Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 60
Sabendo que as porções AC e BC do cabo ACB devem ser iguais, determine o menor comprimento do cabo que pode ser usado para suportar a carga mostrada se a tração no cabo não puder exceder 870 N.
Passo 1
Tá legal, vamos lá! Antes de começar o exercício, é sempre bom ter em mente as dicas que o próprio livro nos dá antes de cada seção de exercícios, na parte de “metodologia para resolução de problemas”. Então beleza, seguindo aquelas dicas, vamos começar fazendo o diagrama de corpo livre:
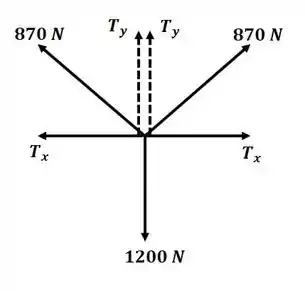
Passo 2
Agora que temos o DCL do problema, e temos quatro forças atuando, vamos tratar o sistema como se a força de 870 N nos cabos fosse decomposta em e , então, nesse caso, aplicando o somatório de forças em :
Agora, como temos o valor da componente e da resultante, podemos encontrar o valor de aplicando pitágoras:
E, substituindo os valores, temos:
Passo 3
Agora, com base na figura a seguir:
Que representa o cabo BC, vamos aplicar semelhança de triângulos entre os triângulos CBD e CEF para obter o valor da distância BC:
Calma! Ainda não acabamos, não podemos nos esquecer de multiplicar esse valor por 2, pois temos o cabo AC ainda, então, o menor comprimento possível para o cabo será: