Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 36

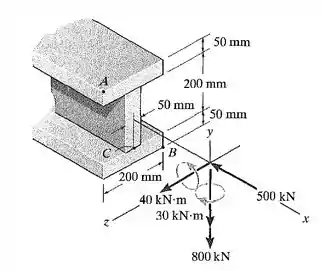
36. As cargas internas em uma seção da viga são mostra das na figura. Determine as tensões principais no ponto A. Calcule também a tensão de cisalhamento máxima no plano nesse ponto

Passo 1

Fala ai meu aprovado, tudo belejóia?

Primeiro, devemos calcular o momento de inércia da seção transversal. Porém, devemos dividir em dois eixos, o eixo y e o eixo z . Sabemos que para seções retangulares, temos a seguinte equação de momento de polar de inércia:

I = 1 12 ( b h 3 )

Onde b é o tamanho da parede paralela ao eixo e h é o tamanho da parede perpendicular ao eixo.

Neste caso, devemos usar o Teorema dos Eixos Paralelos, pois os centroides das peças separadas não estão no mesmo eixo que o centroide da peça total, o qual é dado por:

I T = I + A d 2

Onde a é a área de um elemento separado e d é a distância do seu centroide com o centroide da peça total.

Mas como o centroide da peça 2 coincide com o centroide da peça total, não será preciso aplicar o teorema dos eixos paralelos para ela:

I T z = I P 1 + A 1 d 1 2 + I P 2 + I P 3 + A 3 d 3 2

I P 1 + A 1 d 1 2 = ( 0,2   m ) ( 0,05   m ) 3 12 + 0,2   m × 0,05   m ( 0,125   m ) 2 I P 2 = ( 0,05   m ) ( 0,2   m ) 3 12 I P 3 + A 3 d 3 2 = ( 0,2   m ) ( 0,05   m ) 3 12 + 0,2   m × 0,05   m ( 0,125   m ) 2

Logo:

I T z = ( I P 1 + A 1 d 1 2 ) + ( I P 2 ) + ( I P 3 + A 3 d 3 2 )

I T z ≅ 1,583333 × 10 - 4   m 4 + 0,3333 × 10 - 4   m 4 + 1,583333 × 10 - 4   m 4

I T z ≅ 3,5 × 10 - 4   m 4

Agora, devemos calcular o momento polar de inércia no eixo y . Mas, como o eixo dos centroides das três peças coincidem com o eixo do centroide da peça total, não será necessário o Teorema dos Eixos Paralelos:

I T y = I P 1 + I P 2 + I P 3

I P 1 = ( 0,05   m ) ( 0,2   m ) 3 12 I P 2 = ( 0,2   m ) ( 0,05   m ) 3 12 I P 3 = ( 0,05   m ) ( 0,2   m ) 3 12

I T y ≅ 3,3333 × 10 - 5   m 4 + 0,20833 × 10 - 5   m 4 + 3,3333 × 10 - 5   m 4

I T y ≅ 6,875 × 10 - 5   m 4

Passo 2

Iremos então, calcular a tensão no ponto A , através da seguinte fórmula:

σ A = - N x A - M z y A I z - M y z A I y

σ A = 500 × 10 3   N 0,03   m 2 - 40 × 10 3   k N ⋅ m 0,15   m 3,5 × 10 - 4   m 4 - 30 × 10 3   k N ⋅ m 0,1   m 6,875 × 10 - 5   m 4

σ A = - 77,45   M P a   ( C o m p r e s s ã o )

E em seguida, calcular a tensão máxima de cisalhamento no ponto A :

τ A = V Q A I t

Como Q = 0 , então:

τ A = 0   M P a

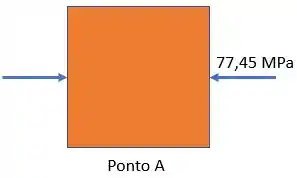
Passo 3

Bora então calcular as tensões principais no ponto A , através da fórmula abaixo:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = ( - 77,45   M P a ) + ( 0   M P a ) 2 ± - 77,45   M P a - ( 0   M P a ) 2 2 + ( 0   M P a ) 2

σ 1,2 ≅ - 38,725   M P a ± 38,725   M P a

Obtemos com isso, duas tensões, σ 1 e σ 2 , sendo assim, para σ 1 :

  σ 1 = σ y ≅ - 38,725   M P a + 38,725   M P a

σ 1 ≅ 0   M P a

Agora para σ 2 :

σ 2 = σ x ≅ - 38,725   M P a - 38,725   M P a

σ 2 ≅ - 77,4   M P a

Passo 4

E por fim, só falta calcular a tensão de cisalhamento máxima no plano τ m á x no ponto A , que se lembrarmos bem, é dada pela fórmula abaixo:

τ m á x = σ x - σ y 2 2 + τ x y 2

τ m á x = ( - 77,45 M P a ) - ( 0   M P a ) 2 2 + ( 0   M P a ) 2

τ m á x ≅ 38,7   M P a

Resposta

As tensões principais no ponto A são:

  σ 1 = σ y ≅ 0   M P a

σ 2 = σ x ≅ - 77,4   M P a

E a tensão de cisalhamento máxima no plano nesse ponto é:

τ m á x ≅ 38,7   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

35. O tubo da perfuratriz tem diâmetro externo de 75m m , espessura de parede de 6m m e pesa 0,8k N / m . Se for submetido a um torque e a carga axial como mostra a figura, determine:(a) as tensões pr
38. Resolva o Problema 9.36 para o ponto C localizado no centro na superfície inferior da alma.
37. Resolva o Problema 9.36 para o ponto B.
O parafuso está preso a seu suporte em C. Se aplicarmos uma força de 90 N à chave para apertá-lo, determine as tensões principais desenvolvidas na haste do parafuso no ponto A. Represente os resultado