Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 35
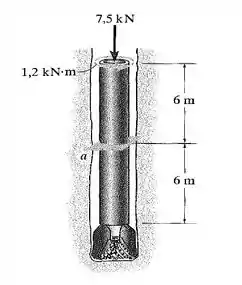
35. O tubo da perfuratriz tem diâmetro externo de , espessura de parede de e pesa . Se for submetido a um torque e a carga axial como mostra a figura, determine:
(a) as tensões principais e
(b) a tensão de cisalhamento máxima no plano em um ponto sobre a sua superfície na seção .
Passo 1
Salve salve meu aprovado, tudo beleza?
Se liga só, nesse exercício aqui o enunciado nos diz que o tubo da perfuratriz tem diâmetro externo de , espessura de parede de e pesa .
Então se ele for submetido a um torque e uma carga axial como mostrado na figura, o enunciado quer que a gente determine (a) as tensões principais e (b) a tensão de cisalhamento máxima no plano em um ponto sobre a sua superfície na seção .
Belezoca, vamos primeiro montar o diagrama de esforço cortante e momento fletor:
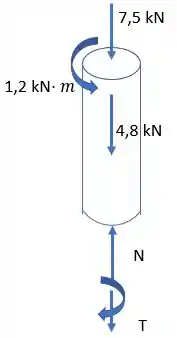
O valor de 4,8 kN foi calculado com a informação dada no enunciado. Como a distância até a seção pela parte de cima é de , basta multiplicar o valor da cara distribuída pela distância .
Agora é só realizar a análise dos esforços cortantes e momento fletor:
E para as forças:
Passo 2
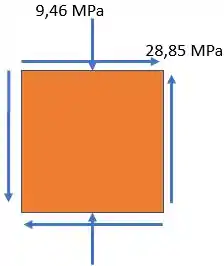
E agora, vamos realizar o cálculo da tensão de um ponto na superfície , dada a fórmulazinha:
Sendo assim, obtemos que:
E em seguida, o cálculo da tensão máxima de cisalhamento de um ponto na nossa superfície:
Passo 3
(a) Obtidas as tensões de estado plano já podemos calcular, então, as tensões principais; que são dadas pela fórmula abaixo:
Obtemos duas tensões, onde uma vai ser máxima, e outra vai ser mínima, , logo para :
Agora para
Passo 4
(b) E por fim, vamos calcular a tensão de cisalhamento máxima no plano :
Resposta
(a) Tensões principais de um ponto na superfície :
(b) Tensão de cisalhamento máxima de um ponto na superfície :