Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 41

O parafuso está preso a seu suporte em C. Se aplicarmos uma força de 90 N à chave para apertá-lo, determine as tensões principais desenvolvidas na haste do parafuso no ponto A. Represente os resultados em um elemento localizado nesse ponto. A haste tem 6 mm de diâmetro

Passo 1

Aqui, vamos primeiro montar o diagrama de esforço cortante e momento fletor do parafuso com um corte no ponto A mas com a chave acoplada, pois a força de 90   k N influencia nas contas:

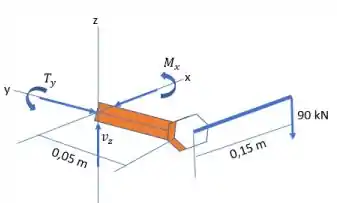
Agora é só realizar a análise dos esforços cortantes e momento fletor:

↑ + ∑ F z = 0 → V z - 90   N = 0   ∴ V z = 90   N

↶ + ∑ M x = 0 → M x = 90   N × 0,05   m ∴ M x = 4,5   N ⋅ m

↶ + ∑ M y = 0 → T y = 90   N × 0,15   m ∴ T y = 13 , 5   N ⋅ m

Passo 2

Agora, calcularemos a tensão no ponto A , lembrando que a fórmula do momento polar de inércia de um círculo é da por π c 4 / 4 , onde c é a distância do centro até a bora mais externa:

σ A = M x y A I x

σ A = ( 4,5   N ⋅ m ) ( 0,003   m ) π 4 ( 0,003   m ) 4

∴ σ A = 212,21   M P a   ( T r a ç ã o )

Cálculo da tensão máxima de cisalhamento no ponto A :

τ A = T y c J

τ A = ( 13 , 5   N ⋅ m ) ( 0,003   m ) π 2 ( 0,003   m ) 4

∴ τ A = 318,31   M P a

Passo 3

Calcularemos, então, as tensões principais no ponto A :

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = 212,21   M P a + 0   M P a 2 ± 212,21   M P a + 0   M P a 2 2 + ( 318,31   M P a ) 2

σ 1,2 = 106,105 M P a ± 335,53   M P a

σ 1 = 441,63   M P a

σ 2 = - 229,42   M P a

Passo 4

Neste passo, vamos encontrar o ângulo θ p que o elemento será rotacionado:

t g 2 θ p = τ x y ( σ x - σ y ) / 2

t g 2 θ p = 318,31   M P a ( 212,21   M P a - 0   M P a ) / 2

t g 2 θ p = 3

E devemos calcular o arco tangente do valor encontrado:

tg - 1 ⁡ 2 θ p = 3

∴ θ p 1 = 35,78 °

Esse ângulo é quanto um dos eixos está deslocado, para achar o outro, devemos somar noventa graus:

θ p 2 = 35,78 ° + 90 ° = 125,78 °

Passo 5

Por fim, vamos utilizar a fórmula a seguir para descobrir qual tensão das duas achadas é a tensão que está deslocada no eixo x :

σ x ' = σ x + σ y 2 + σ x - σ t 2 ⋅ cos ⁡ 2 θ + τ x y ⋅ s e n ( 2 θ )

σ x ' = 212,21     M P a 2 + 212,21 M P a 2 ⋅ cos ⁡ 2 35,78 ° + 318,37   M P a ⋅ s e n ( 2 ( 35,78 ° ) )

∴ σ x ' = 441,63   M P a

Resposta

As tensões principais desenvolvidas no ponto A da haste do parafuso são:

σ 1 = 441,63   M P a

σ 2 = - 229,42   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

49. A viga-caixão está sujeita às cargas mostradas na figura. Determine as tensões principais na viga no ponto A e no ponto B .
51. As cargas internas em uma seção da viga consistem em uma força axial de 500N , uma força de cisalhamento de 800N e duas componentes de momento 30N ⋅ m e 40N ⋅ m . Determine as tensões principais n
48. A extremidade da viga em balanço está sujeita à carga mostrada. Determine as tensões principais na viga nos pontos A e B .
As cargas internas em uma seção da viga consistem em uma força axial de 500N , uma força de cisalhamento de 800N e duas componentes de momento 30N ⋅ m e 40N ⋅ m . Determine as tensões principais no po
As tensões principais em um ponto são mostradas na figura. Se o material for alumínio, para o qual E a l = 70G P a e v a l = 0,33 , determine as deformações principais.