Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 41
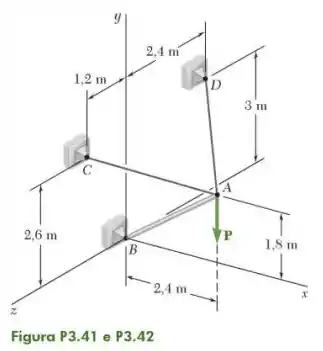
41- Sabendo que a tensão no cabo é , determine o ângulo entre o cabo e a barra , a projeção em da força exercida pelo cabo no ponto .
Passo 1
Para encontrar o ângulo entre e não precisaremos da força, somente do comprimento dessas barras e de suas representações vetoriais. Para que possamos utilizar na seguinte fórmula abaixo:
Lembrando que os dois vetores tem que sair do mesmo ponto.
Começando por temos:
Cujo comprimento será:
E para :
Cujo comprimento será:
Passo 2
Logo o ângulo formando entre essas linhas será de:
Isso será:
Passo 3
Como temos o ângulo entre e , e temos a força em , logo para achar a componente dessa força em basta fazer o cosseno da força em , ou seja.
Resposta
Exercícios de Livros Relacionados
2.12. O dispositivo é usado para a substituição cirúrgica da articulação do joelho. Se a força que atua ao longo da perna é 360N , determine suas componentes ao longo dos eixos x e y ' .
2.13. O dispositivo é usado para a substituição cirúrgica da articulação do joelho. Se a força que atua ao longo da perna é 360N , determine suas componentes ao longo dos eixos x ' e y .
2.31. Três cabos puxam um tubo de tal modo que geram uma força resultante com intensidade de 1800N . Se dois dos cabos estiverem submetidos a forças conhecidas, como mostra a figura, determine o ângul
2.22. Se Φ = 30 ° , F 1 = 5k N e a força resultante deve ser orientada ao longo do eixo y positivo, determine a intensidade da força resultante, se F 2 necessita ser mínima. Além disso, quais valores
2.24. Se a força resultante F R está orientada ao longo da linha a 75° no sentido horário a partir do eixo x positivo e a intensidade de F 2 deve ser mínima, determine as intensidades de F R e F 2 , e