Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 39
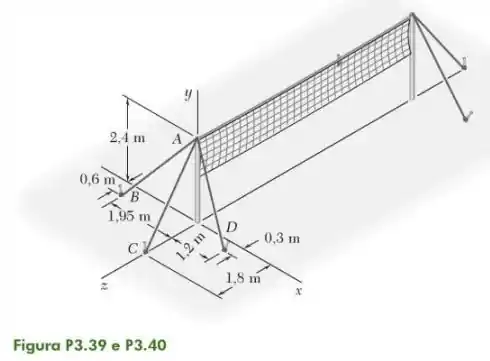
39- Considere a rede de voleibol mostrada na figura. Determine o ângulo formado pelos cabos de sustentação e .
Passo 1
Basicamente se quer o ângulo formado entre os cabos e e para isso precisamos saber as representações vetoriais de e .
Considerando os vetores começando em temos:
E o módulo desse vetor será:
Agora o vetor será:
E o módulo será:
Passo 2
Dessa forma pela definição do vetor escalar temos:
Logo:
O que será:
Em graus temos o ângulo igual a:
Resposta
Exercícios de Livros Relacionados
Duas forças P e Q são aplicadas no ponto A de um suporte tipo gancho. Sabendo que P = 266N e Q = 110N , determine graficamente a intensidade, a direção e o sentido da resultante usando (b) a regra do
Para o suporte tipo gancho do Problema 2.7, determine usando trigonometria, (a) a intensidade e a direção da menor força P para que a resultante R das duas forças aplicadas no suporte seja horizontal,
Um tanque de aço deve ser posicionado em uma escavação. Sabendo-se que a intensidade de P = 2220N , determine, usando a trigonometria, (a) o ângulo requerido se a resultante R das duas forças aplicada
A força de 1.330N deve ser decomposta em componentes ao longo das linha a - a ' e b - b ' . (a) Usando trigonometria, determine o ângulo α sabendo que o componente ao longo de a - a ' é 530N , (b) Qua
Duas forças P e Q são aplicadas no ponto A de um suporte tipo gancho. Sabendo que P = 266N e Q = 110N , determine graficamente a intensidade, a direção e o sentido da resultante usando (a) a lei do pa