Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 38
38. A treliça mostrada na figura consiste em nove elementos e é sustentada por uma rótula em , por duas pequenas hastes de conexão em e uma pequena haste de conexão em . Determine a força em cada membro para o carregamento dado:
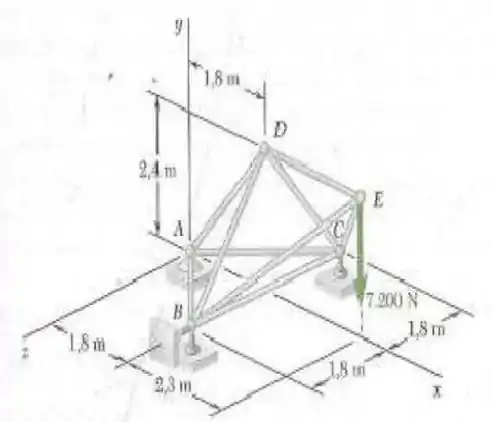
Passo 1
Bom! Primeiramente vamos fazer o esboço de todas as forças presentes no nosso sistema, o chamado diagrama de corpo livre:
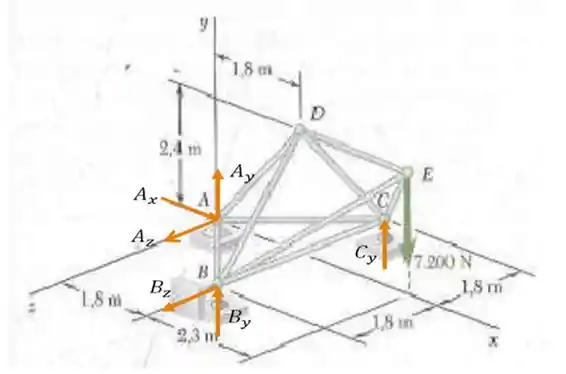
Olhando essa belezinha de figura, de cara já podemos tirar algumas relações:
E também, como as seguintes condições precisam ser satisfeitas:
De modo que a força é dada por:
E pela figura, por simetria, tiramos que:
Façamos o somatório das forças em :
Passo 2
Agora, faremos o diagrama de corpo livre para o ponto do sistema:
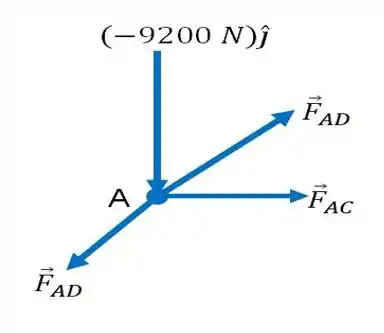
Antes de mais nada, vamos definir algumas coordenadas de interesse para nossa análises. São as coordenadadas dos pontos , , , e :
Fizemos isso, para obter as forças presentes no ponto feitas em nossa análise, as quais são obtidas através das seguintes relações:
Onde para encontrar cada vetor posição, por exemplo no caso de , basta subtrair as coordenadas de pela de . Já no caso de , basta subtrair as coordenadas de pela de e o mesmo ocorre para . Chega de papo e partiu fazer os cálculos:
E como o somatório vetorial das forças precisa ser zero, então temos que:
Passo 3
Agora, que já temos mais ou menos uma idéia da aparência das forças no ponto do nosso sisteminha e sabemos que o somatório vetorial delas resulta em zero, vamos fazer o somatório separado das forças em cada componente cartesiano, , e ; já que ele necessariamente também tem que dar zero. Vamos lá:
Primeiro para a componente :
Segundo para a componente :
Terceiro para a componente :
Como obtemos na equação , que ; vamos tratar de usar essa relação em :
E não vamos nos esquecer que:
Passo 4
Em seguida, vamos fazer a análise do diagrama de corpo livre para o ponto :
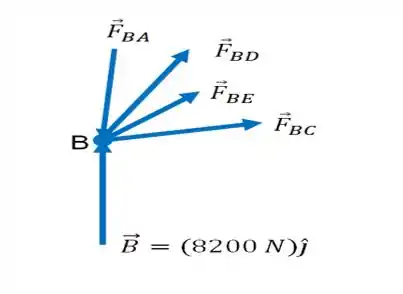
O somatório vetorial das forças disso precisa ser zero, então temos que:
E novamente repetiremos o mesmos raciocínio dos e :
Separando as componentes cartesianas logo em seguida, obtemos os seguintes resultados:
Para :
Para :
Para :
Teríamos que obter a força também. Só que para nossa imensa felicidade essa força é simétrica à força , o que implica dizer que elas são iguais. Logo, temos que .
Passo 5
Falta apenas analisar o ponto . Se repararmos bem, há apenas duas forças atuando nesse ponto, a força e a força que teoricamente queríamos obter, . A força nos outros elementos a gente desconsidera, já que e são simétricos de modo que as forças neles, se anulam.Desse jeito, para obter , façamos o somatório das forças na direção horizontal :