Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 50

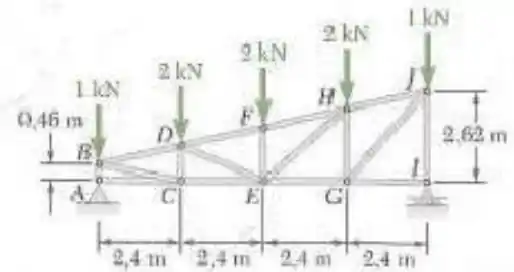
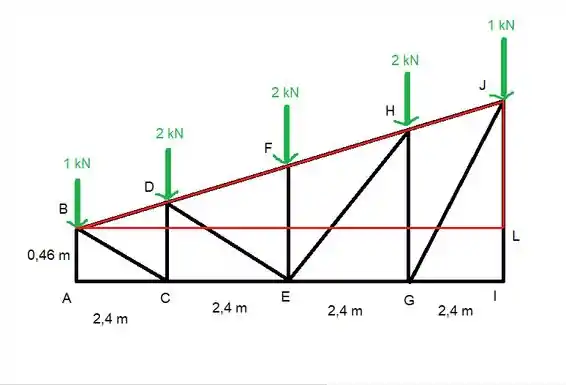
6.50. Uma treliça de telhado de uma água é carregada tal como mostra a figura. Determine a força nos elementos EG, GH e HJ.

Passo 1

Vamos fazer o desenho disso

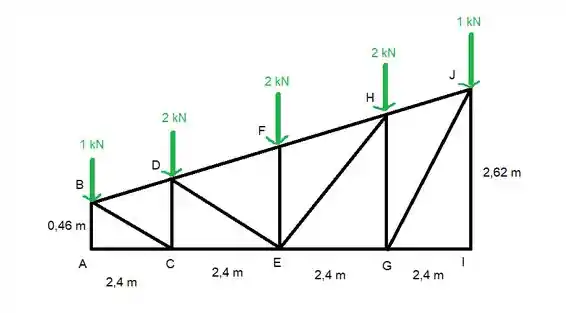
O que a gente consegue tirar só da imagem são as forças de reação nas pontas

A x = I x = 1 2 ∑ F x = 0

E

A y = I y = 1 2 ∑ F y = 4   k N

Passo 2

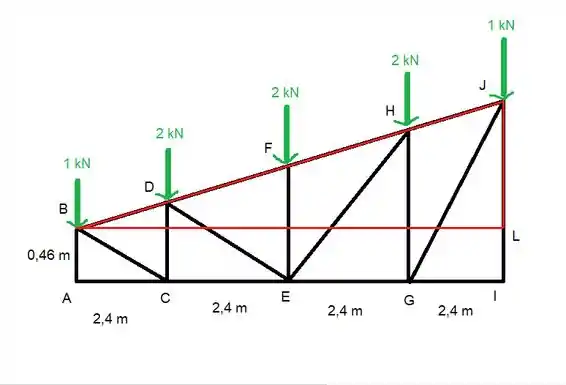
O melhor que a gente pode fazer aqui é usar o método das seções, vamos seccionar desse jeito

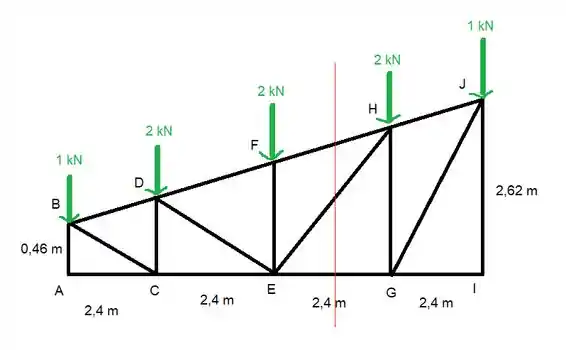
E aí a gente tem

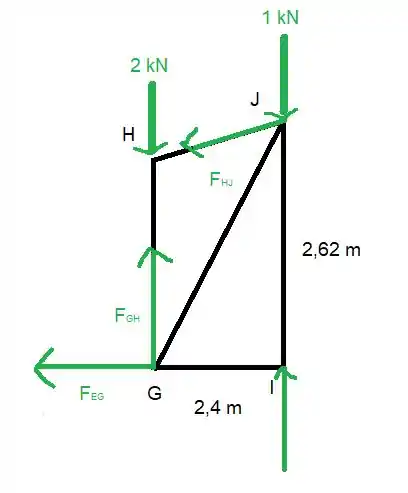
A gente pode determinar aquela distancia G H - usando propriedade de semelhança de triângulos.

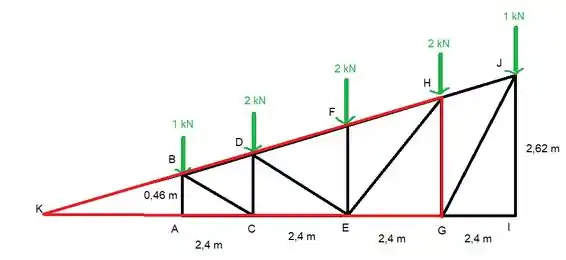
Podemos fazer isso desde que o ângulo L B ^ J seja o mesmo que o ângulo G K ^ H .

Então a gente tem que

G H - K G - = L J - B L -

A gente pode determinar L J -

L J - = I J - - A B - = 2,62 - 0,46 = 2,16

E também

B L - = 4 ⋅ 2,4 = 9,6

Mas para determinar K G - precisamos determinar K A -

A gente pode determinar aquela distancia K A - usando propriedade de semelhança de triângulos.

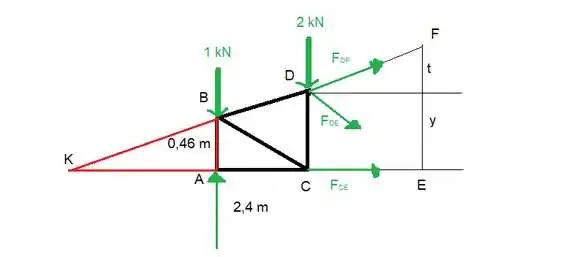
Então a gente tem que

A B - K A - = L J - B L -

Então vamos isolar K A -

K A - = B L - L J - ⋅ A B - = 9,6 2,16 ⋅ 0,46 = 2,044   m

Então

K G - = 2,044 + 3 ⋅ 2,4 = 9,244

Agora podemos fazer

G H - = L J - B L - K G -

G H - = 2,16 9,6 ⋅ 9,244 = 2,08   m

Passo 3

Beleza, agora a gente pode calcular os momentos, vamos usar o momento no ponto H.

∑ M H = 0

I x ⋅ 2,4 - 1 ⋅ 2,4 - F E G ⋅ 2,08 = 0

Mas I x = 4   k N

F E G = 3,4615   k N

E como é positivo, nossa representação do vetor está correta e é uma força de tração.

Agora para achar F G H vamos usar o momento em J

∑ M J = 0

- F G H ⋅ 2,4 - F E G ⋅ 2,62 = 0

Logo

F G H = - 3,7788   k N

E como a força é negativa, a força é de compressão.

E agora para determinar F H J não vamos usar momento, vamos usar somatório das forças, mas para isso precisaremos da componente em x de F H J .

Beleza agora vamos determinar t e y

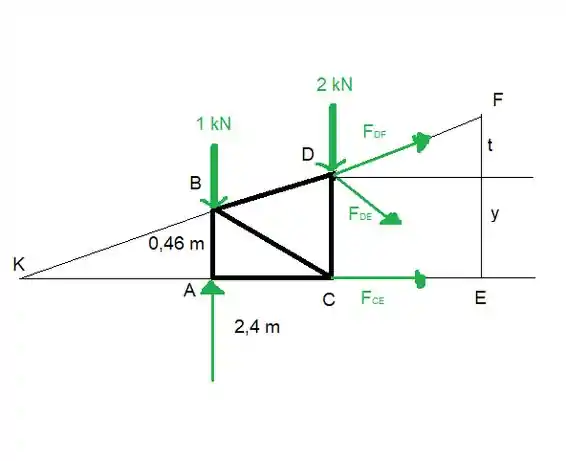
Bem, y = C D - = 1 , agora vamos determinar E F - para chegar em t

E F - K E - = L J - B L -

E F - = 2,16 9,6 ⋅ 2,0444 + 2,4 + 2,4 = 1,54

Então

t = E F - - y = 0,54

Agora temos

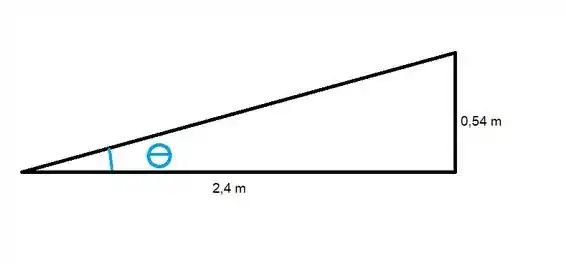
Agora vamos fazer a hipotenusa

D F - = 2,4 2 + 0,54 2 = 2,46

Então

F H J x = F H J ⋅ cos ⁡ θ = 2,4 2,46 F H J

Voltando

∑ F x = - F E G - 2,4 2 , 4 6 F H J = 0

Isolando F H J

F H J = - 2,46 2,4 F E G = - 3,548   k N

E como é negativo, é um força de compressão.

Resposta

F E G = 3,4615   k N

F G H = - 3,7788   k N

F H J = - 2,46 2,4 F E G = - 3,548   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

105- Para a estrutura e carregamento mostrado na figura, determine os componentes das forças atuantes no elementos D A B C em B e D .
109- Sabendo que nas superfícies em A e D não há atrito, determine as forças exercidas em B e C no elemento B C E .
116- Resolva o Problema 6.114 considerando que a força P é substituída por um binário no sentido horário de momento M 0 aplicado ao elemento C D E em D .
112- Os elementos A B C e C D E são ligados por pinos em C e sustentados por quatro hastes. Para o carregamento mostrado nas figuras, determine a força em cada haste.
115- Resolva o Problema 6.113 considerando que a força P é substituída por um binário no sentido horário de momento M 0 aplicado ao elemento C D E em D .