Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 40
40. Determine a força nos membros , e da treliça e indique, se os membros estão sob tração ou compressão.
Passo 1
Para começar a resolver o problema, vamos analisar o digrama de corpo livre da seção que sofreu o corte que passa pelos membros citados no enunciado.
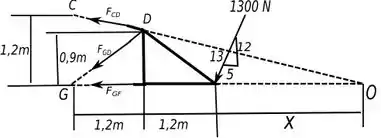
Esse ponto mostrado na figura foi definido com o intuito de facilitar nossas análises.
Para determinar a distância , basta fazer uma igualdade de triângulos da seguinte maneira:
Inicialmente vamos considerar todas as forças como sendo de tração, caso alguma apareça de forma negativa, saberemos que ela não é de tração mais sim de compressão.
Vamos usar as equações de equilíbrio para o momento para acharmos as forças que queremos.
Passo 2
Para usarmos as equações de equilíbrio precisamos decompor nossas forças em suas componentes, mas para fazer isso precisamos saber os ângulos que essas forças , fazem com a horizontal.
Como elas fazem parte de triângulos, podemos achar esses ângulos por trigonometria simples.
Primeiro vamos fazer para , o triangulo que ela pertence é:
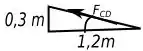
Então:
Agora vamos fazer para , o triangulo que ela pertence é:
Então:
Agora que temos esses ângulos, podemos usar nossas forças da forma que quisermos.
Passo 3
Vamos aplicar as equações de equilíbrio.
Vamos começar com o ponto , já que e não contribuem para o momento em .
Então:
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Passo 4
Agora vamos analisar o ponto para encontrarmos .
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Passo 5
Agora vamos analisar o ponto para encontrarmos .
Como o resultado foi positivo, essa força é realmente uma força de tração.