Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 51
51. Determine a força em cada membro da treliça e indique se os membros sob tração ou compressão. Faça , .
Passo 1
Para resolver esse problema vamos primeiro analisar o diagrama de corpo livre da treliça como um todo, para achar as forças que atuam nos pontos e , pois precisaremos delas para encontrar as outras forças que queremos.
Para isso vamos usar as equações de equilíbrio referentes ao momento e referentes a força.
Feito isso vamos utilizar o método dos nós em todos os nós da treliça, para assim conseguirmos o que o enunciado pede.
Inicialmente vamos considerar todas as forças como sendo de tração, caso alguma apareça de forma negativa, saberemos que ela não é de tração, mas sim de compressão.
Passo 2
Vamos analisar o diagrama da treliça com um todo.
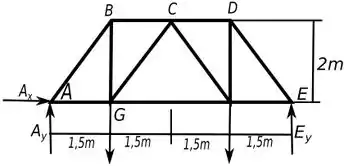
Com isso vamos determinar primeiro
Agora vamos achar :
Agora vamos achar :
Passo 3
A parti de agora vamos usar o método dos nós em cada nó da treliça.
Vamos começar com o ponto , abaixo temos o diagrama de forças desse ponto.
Temos:
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Como o resultado foi positivo, essa força é realmente uma força de tração.
Passo 4
Vamos agora com o ponto , abaixo temos o diagrama de forças desse ponto.
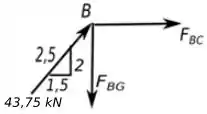
Temos:
Como o resultado foi positivo, essa força é realmente uma força de tração.
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Passo 5
Vamos agora com o ponto , abaixo temos o diagrama de forças desse ponto.
Temos:
Como o resultado foi positivo, essa força é realmente uma força de tração.
Como o resultado foi positivo, essa força é realmente uma força de tração.
Passo 6
Vamos agora com o ponto , abaixo temos o diagrama de forças desse ponto.
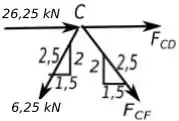
Temos:
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Passo 7
Vamos agora com o ponto , abaixo temos o diagrama de forças desse ponto.
Temos:
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Como o resultado foi positivo, essa força é realmente uma força de tração.
Passo 8
Vamos agora com o ponto , abaixo temos o diagrama de forças desse ponto.
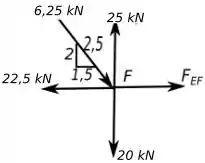
Temos:
Como o resultado foi positivo, essa força é realmente uma força de tração.