Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 55
55. A treliça espacial suporta uma força . Determine a força em cada membro e indique se os membros estão sob tração ou compressão.
Passo 1
Inicialmente vamos considerar todas as forças como sendo de tração, caso alguma apareça de forma negativa, saberemos que ela não é de tração, mas sim de compressão.
Vamos analisar cada ponto separadamente e utilizar as equações de equilíbrio referentes as forças em cada direção.
Para isso vamos usar as componentes das forças em cada direção e isso pode ser feito se você observar que elas fazem parte de triângulos retângulos, mas especificamente, são as hipotenusas, logo podemos expressar suas componentes através de proporção entre os lados do triângulo.
Passo 2
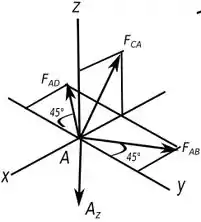
Vamos começar analisando o ponto , abaixo tem um diagrama de forças que mostra a situação.
Resolvendo o sistema das duas equações que encontramos, ficamos com:
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Como o resultado foi positivo, essa força é realmente uma força de tração.
Passo 3
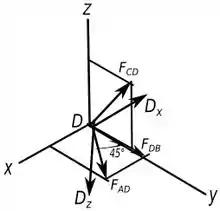
Vamos analisar o ponto , abaixo tem um diagrama de forças que mostra a situação.
Como o resultado foi positivo, essa força é realmente uma força de tração.
Logo:
Passo 4
Vamos analisar o ponto , abaixo tem um diagrama de forças que mostra a situação.
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.