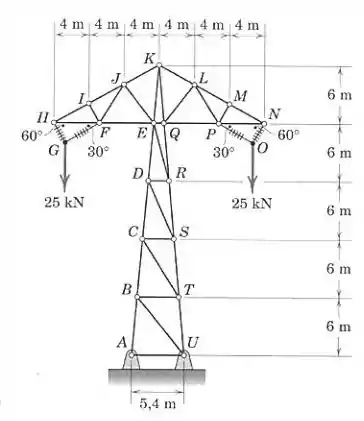
Um modelo de projeto para uma torre de linha de trans,issão está mostrado na figura. Os elementos , , e são cabos isolados; todos os outros elementos são barras de aço. Para o carregamento mostrado, calcule as forças nos elementos , , , e . Use uma combinação de métodos se desejado.

Primeiro queremos achar a força . Ela é a mais fácil de ser encontrada, porque se olharmos para o nó vemos que já que não há nenhuma outra barra que possa equilibrar uma força feita por esse elemento na direção perpendicular a e .

A segunda força que queremos achar é . Vamos tentar calcular a partir do nó . Não escrevemos a força pois já sabemos que ela é nula:

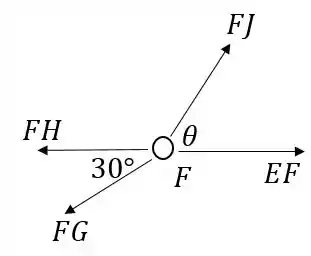
Na direção temos apenas duas forças, então se acharmos podemos encontrar com uma equação. Também precisamos encontrar o ângulo . Vamos então por partes, primeiro calculando a força , depois o ângulo, e depois aplicando a equação. Através do nó :

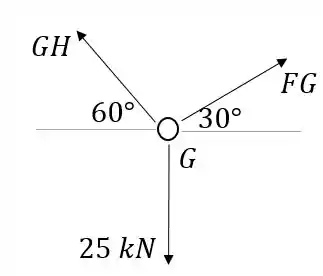
Pelo equilíbrio na direção achamos uma relação entre e :

Agora achamos pelo equilíbrio na direção , substituindo por :

Também achamos a força :

Falta achar o ângulo . Vamos analisar melhor o desenho da treliça nessa parte. O Ângulo de inclinação das barras de , e e, relação à horizontal é:

Então, se é perpendicular a e , o ângulo entre e a horizontal é .

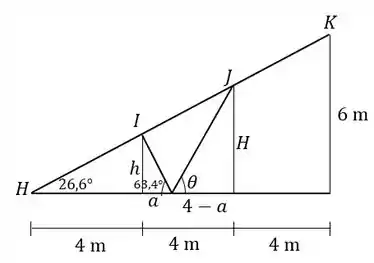
Acharemos o ângulo através de sua tangente, dada por

Primeiro achamos as alturas e pela semelhança de triângulos:

Então encontramos o valor de :

Calculamos a tangente de :

E então o ângulo :

Tendo o valor de e do ângulo , agora podemos voltar a olhar para o nó , e calcular :

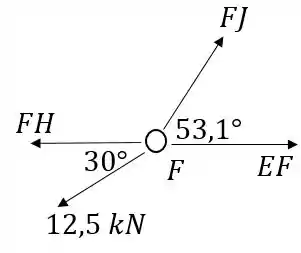
Pelo equilíbrio em :

Vamos agora tentar calcular . Vamos calcular essa pelo método das seções. Queremos fazer um corte na treliça que passe por . Vamos cortar então , e . Nosso pedaço da treliça é então esse aqui:

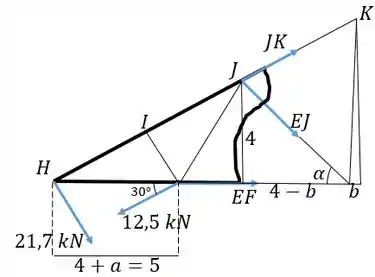
Se calcularmos o momento em torno de e não aparecem, então é isso que vamos fazer. Precisamos antes do ângulo que faz com a horizontal. O calculamos através de sua tangente. A distância é calculada por semelhança de triângulos, para o grande triângulo no meio da treliça. Temos:

Então calculamos a tangente de e logo em seguida o próprio ângulo:

Podemos então fazer ser zero o momento em torno de :

Calculando os valores do seno e do cosseno e multiplicando:

O sinal negativo indica que a força é de compressão, e não de tração como desenhamos.

Vamos então partir para o cálculo de . Podemos fazer isso pelo método dos nós em . Esse ponto é mais fácil por conta da simetria, que faz termos as seguintes igualdades:

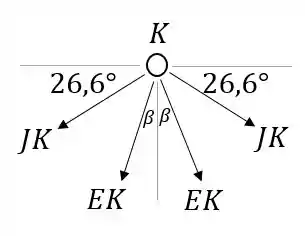
Precisamos do valor de e do ângulo para calcular . Vamos voltar para o corte que fizemos anteriormente, pois lá também tínhamos a força :

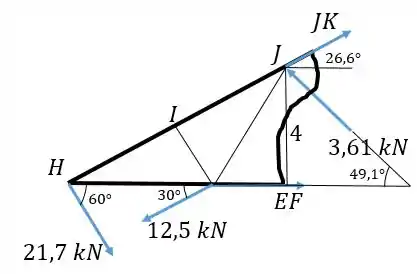
Agora com o valor já representado no sentido correto, fazemos a soma das forças em para obter :

Calculando os senos e multiplicando:

O ângulo é calculado através de sua tangente:

Tendo em mãos os valores de e , agora podemos calcular no nó :

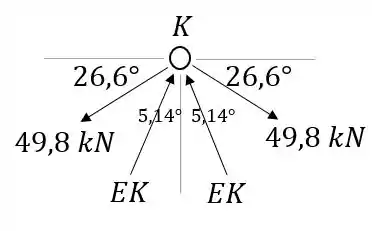
Pelo equilíbrio na direção :

Só falta calcular . Pelo método das seções, podemos isolar o triângulo grande superior da treliça . Vamos considerar que as cargas de 25 kN são aplicadas em um ponto entre e na esquerda e e na direita. As forças que atuam nesse triângulo são as cargas de 25 kN, e as forças dos elementos , e :

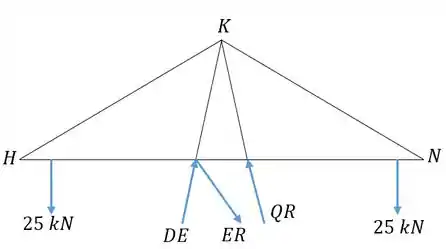
Agora devemos perceber que o momento em relação a feito pelas duas forças de 25 kN se anulam, e as forças e não aplicam momento por terem linha de ação passando pelo ponto. Logo, para o momento total ser zero a força deve ser zero: