Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 5ª Edição - Russel C. Hibbeler- Ed: 5º - Capítulo 9.Problemas - Ex. 41
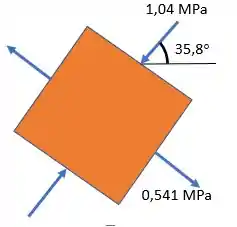
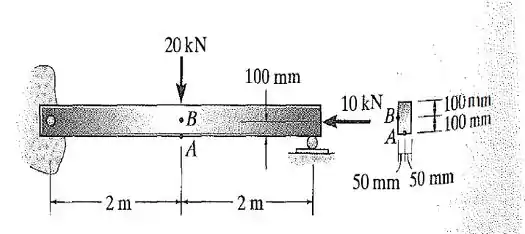
43. A viga tem seção transversal retangular e está sujeita às cargas mostradas. Determine as tensões principais desenvolvidas no ponto e no ponto , localizado imediatamente à esquerda da carga de . Mostre os resultados em elementos localizados nesses pontos.
Passo 1
Vamos primeiro, então, montar os diagramas de corpo livre da viga:
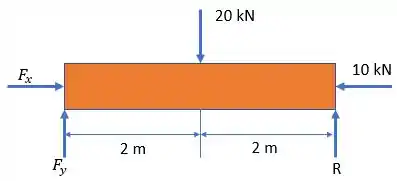
E realizar o somatório de momentos em relação ao pino e forças horizontais e verticais em relação ao pino no lado esquerdo:
Feito isso, vamos fazer o diagrama de esforço cortante e momento fletor a partir do lado esquerdo da viga e com o corte no ponto ou (ou ):
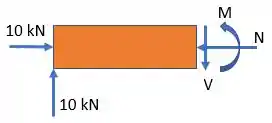
Agora é só a gente fazer a análise dos esforços cortantes e momento fletor:
Passo 2
Como calculamos os resultados comuns aos dois pontos que pede o enunciado, iremos dividir a questão, resolvendo primeiro que foi pedido para o ponto e depois para o ponto .
Vamos calcular a tensão no ponto , lembrando que a fórmula do momento polar de inércia de um retângulo é onde é o tamanho da parede paralela ao eixo e é o tamanho da parede perpendicular ao eixo e que o valor de “” é a distância da linha neutra da seção transversal até o ponto:
E também a tensão máxima de cisalhamento no ponto :
Como :
Passo 3
Com isso, a gente vai calcular agora, as tensões principais no ponto :
Essa fórmula nos fornece duas tensões, uma máxima e uma mínima :
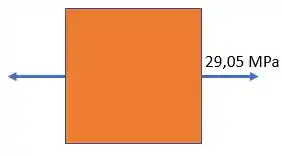
Passo 4
Enfim, vamos achar o ângulo que o elemento será rotacionado:
E devemos calcular o arco tangente do valor encontrado:
Esse ângulo é quanto um dos eixos está deslocado. Para achar o outro, devemos somar noventa graus com o primeiro:
Isso indica que nenhum dos eixos estão deslocados em relação aos eixos originais.
Passo 5
Aqui, vamos repetir todos os passos anteriores para o ponto .
Primeiro, o cálculo da tensão no ponto :
Cálculo da tensão máxima de cisalhamento no ponto :
Passo 6
E agora, o cálculo das tensões principais no ponto , pela fórmula:
Novamente obtemos duas tensões, uma máxima e uma mínima :
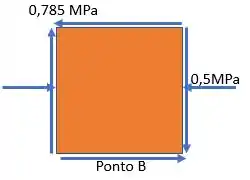
Passo 7
Agora, vamos achar o ângulo que o elemento será rotacionado:
E devemos calcular o arco tangente do valor encontrado:
Esse ângulo é quanto um dos eixos está deslocado. Para achar o outro, devemos somar noventa graus com o primeiro ângulo :
Resposta
Tensões principais no ponto :
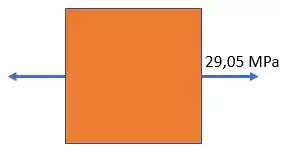
Tensões principais no ponto :
