Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 18
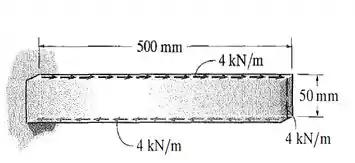
18. A barra de aço tem espessura de 12 mm e está sujeita à carga periférica mostrada na figura. Determine as tensões principais desenvolvidas na barra.
Passo 1
Ora bolas! Se a própria questão diz que a barra está sujeita apenas a uma carga periférica, é meio na cara que a única tensão atuando em um elemento qualquer da barra, é a tensão cisalhante . Vamos então, tratar de calculá-la.
Passo 2
Se a barra tem uma densidade de força constante periférica igual a , bora calcular quanto vale essa força ao longo de toda a barra? Para fazer isso, basta multiplicar a densidade de força pelo comprimento total do nosso objeto, de modo que ficamos com:
Agora que já obtemos a força, para encontrar a tensão cisalhante basta dividir a força pela área da seção transversal da barra e achamos nosso .
Considerando que adotemos como nosso elemento para estado plano, um ponto da seção transversal da barra, então nossa representação vai ficar assim:
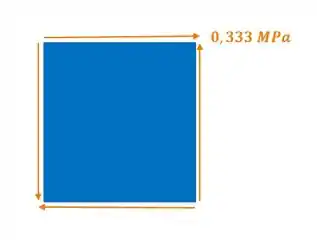
Onde:
Passo 3
Finalmente, só nos resta aplicar a fórmula das tensões principais para encontrar nossa resposta. Sabemos que ela tem a seguinte cara:
Substituindo os valores numéricos adequados, chegamos até:
Pera só um pouco que ainda não terminou! O enunciado pede as “tensões principais”, no plural. Se repararmos bem tem um ali, no nosso último cálculo . Isso significa que um resultado vai ter valor máximo e outro vai ter valor mínimo. Concluímos então, que vamos obter duas tensões, uma máxima e outra mínima . Voltemos aos nossos cálculos, para obter o resultado, de fato: