16. O estado de tensão em um ponto é mostrado no elemento. Determine:
(a) as tensões principais e
(b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação do elemento em cada caso.
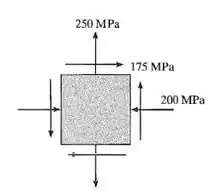
Passo 1
Da figura do enunciado, que mostra um estado plano de tensão, tiramos que:
Passo 2
(a) Agora, dado que temos os valores de , e , vamos encontrar as tensões principais como pede o enunciado:
Sabemos que a fórmula das tensões principais tem a seguinte cara:
Concluímos então, que vamos obter duas tensões, uma máxima e outra mínima . Voltemos aos nossos cálculos, para obter o resultado.
Agora, vamos tratar de encontrar o ângulo, em que nosso elemento vai estar orientado no plano. Sabe-se que a fórmula dele é dada por:
Bem! Já conhecemos o valor de , e . Só falta substituí-los na fórmula do nosso ângulo:
Esse é o ângulo responsável pela tensão principal máxima .
Mas e o outro ângulo, responsável pela tensão principal mínima ?
Aí é so lembrar que os dois ângulos estão relacionado por . Basta então, somar com , para obter o valor de :
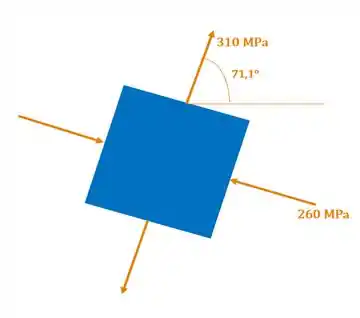
Passo 3
(b) Esse letra é meio curiosa, porque já resolvemos ela praticamente inteira na letra (a). Quer ver só?
A fórmula da tensão de cisalhamento máximo no plano, é dada pela letra e igual a:
Viu só, fizemos esse cálculo na letra (a) e a resposta foi, trocando os valores numéricos adequados, igual a:
E a tensão normal média? Também já resolvemos ela na letra (a). Se não acredita, veja só!
A fórmula da tensão normal média ,é igual a:
Também já fizemos esse cálculo na letra (a) e a resposta foi :
Agora só falta, encontrar o ângulo de cisalhamento no plano. Sabemos que ele tem a seguinte cara:
Vamos substituir os valores numéricos adequados e encontrar nosso ângulo:
Se fossemos representar esse ângulo de cisalhamento em um plano, juntamente com a tensão cisalhante máxima e a tensão normal média iríamos obter a seguinte imagem:
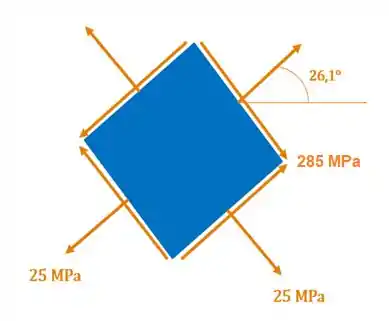
Para encontrar o nosso outro ângulo de cisalhamento , basta subtrair , que é positivo, de .
Resposta
(a)
(b)