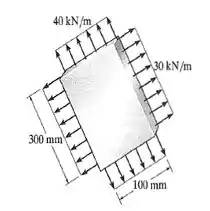
19. Uma placa de aço tem espessura de 10 mm e está sujeita à carga periférica mostrada na figura. Determine a tensão de cisalhamento máxima no plano e a tensão normal média desenvolvidas no aço.

Dado que a nossa placa está sujeita a cargas periféricas, que são perpendiculares à sua superfície concluímos que as únicas tensões agindo no nosso sistema, são as tensões normais. Atenção hein! Aqui, nada de tensão cisalhante. Chamando de a tensão relativa à carga de e de , a tensão relativa à carga de , vamos então, calculá-las.

A tensão normal é dada pela divisão da força total atuante perpendicular, ,pela área da superfície em que ela está concentrada, . No caso da carga de , a força é dada pelo produto do comprimento total em que ela está localizada na barra, no caso , pela carga periférica. Logo, chegamos à:

Agora, basta dividir por , para encontrar :

Vamos repetir o mesmo procedimento para encontrar , relativo à carga de . Primeiro tratemos de encontrar a força atuante , dada que a carga age por um comprimento de .

E dividimos por , para encontrar :

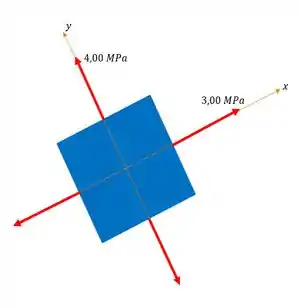
Obtidas nossas tensões normais, não custa nada a gente fazer um esboço do estado plano para nosso elemento, que consideremos como um pequeno ponto da seção transversal. O desenho fica assim:

Partiu então, usar a fórmula da tensão de cisalhamento máximo para o nosso estado plano da figura acima! Sabemos que:

E a fórmula do cisalhamento máximo , é dada por:

Substituindo os valores, obtemos nosso resultado dado como:

Enquanto que será: