Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 50
50. Determine o intervalo de valores admissíveis da tração no arame sabendo que a intensidade do binário no engaste não pode exceder
Passo 1
O que o enunciado quer, nada mais é que uma faixa de valores que pode assumir, então temos que achar um valor mínimo de e um valor máximo de , conseguindo isso, teremos nossa faixa de valores.
O valor que não podemos ultrapassar pode ser tanto que indica um momento no sentido horário e que indica um momento no sentido anti-horário.
Como queremos valores de , será melhor usarmos a equação de equilíbrio referente ao momento em relação ao ponto , pois assim as forças que atuam em não contribuem para o cálculo do momento.
Mas para começarmos a resolver temos que decompor a força em suas componentes vertical e horizontal para usarmos nas equações de equilíbrio.
Para fazer isso vamos ter que usar a trigonometria ao nosso favor, já que a força está na hipotenusa do seguinte triangulo retângulo.
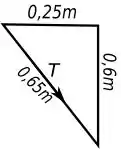
Assim podemos decompor a força da seguinte maneira:
Passo 2
Vamos começar assumido que o valor máximo será , então temos:
Então temos que:
Passo 3
Agora vamos assumir que o valor máximo será , então temos:
Então temos que:
Passo 4
Então encontramos um mínimo de e um máximo de, então o valor pode estar entre esses dois valores.