Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 05
Calcule as forças nas barras , e para a treliça carregada. O elo de restrição é horizontal.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as forças nas barras , e da treliça devido ao peso de aplicado ao nó Antes de resolver, vamos fazer o diagrama de corpo livre da treliça para entender melhor o problema:
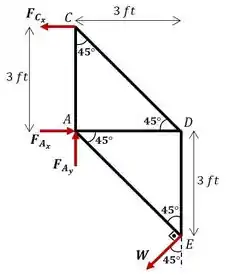
Os ângulos anotados foram obtidos por geometria, uma vez que os triângulos e são isósceles com ângulos retos nas arestas e , respectivamente.
Para descobrirmos o módulo, direção e sentido das forças atuando nas barras, precisamos sempre partir de um ponto/nó que tenha uma força com módulo, direção e sentido conhecidos.
Passo 2
Show! Com isso, podemos analisar os nós da treliça separadamente, que devem estar em equilíbrio para que a treliça também esteja. Começando pelo nó , temos:
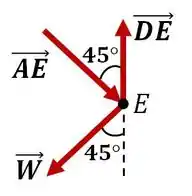
Fazendo o equilíbrio de forças nas direções e :
Sempre que uma força apontar para o nó ela é de compressão , ou seja, tende a comprimir a barra. Se apontar para fora, ela é de tração e tende a alongar a barra.
Passo 3
Tranquilo né? Vamos fazer o mesmo para o nó , que também deve estar em equilíbrio.
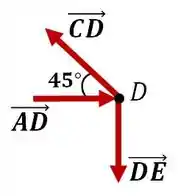
Pelo equilíbrio de forças nas direções e :
Passo 4
E, finalmente, analisando separadamente o nó .
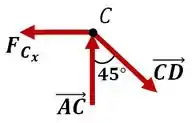
E novamente, o equilíbrio de forças nas direções e :
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 