Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 10
Calcule a força em cada membro da treliça carregada.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força que cada barra da treliça está submetida devido ao carregamento no nó . Antes de resolver, vamos fazer o diagrama de corpo livre da treliça para entender melhor o problema:
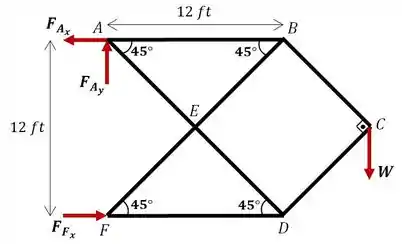
Os ângulos anotados foram obtidos por geometria dos triângulos isósceles e .
Para descobrirmos o módulo, direção e sentido das forças atuando nas barras, precisamos sempre partir de um ponto/nó que tenha uma força com módulo, direção e sentido conhecidos.
Show! Com isso, podemos analisar os nós da treliça separadamente, que devem estar em equilíbrio para que a treliça também esteja. Começando pelo nó :
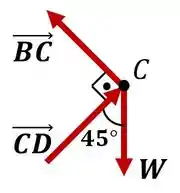
Agora podemos fazer o equilíbrio de forças nas direções e :
Sempre que uma força apontar para o nó ela é de compressão , ou seja, tende a comprimir a barra. Se apontar para fora, ela é de tração e tende a alongar a barra.
Passo 2
Show, feito isso, vamos analisar o nosso problema. Pelo diagrama de corpo livre fica claro que a treliça é totalmente simétrica. Dessa forma, e considerando o sentido da força , podemos concluir que as barras da parte de cima da treliça estarão submetidas às mesmas forças que as barras de baixo, mas em sentido aposto.
Show! Então vamos analisar as barras de cima e espelhar para as de baixo. Repetindo os cálculos do Passo 1 para o nó , temos:
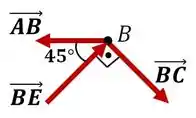
Novamente, utilizando as equações de equilíbrio de força:
Espelhando para as barras de baixo:
Passo 3
Tá quase acabando hein?! Não desiste não!! Hahaha
Agora falta apenas as forças nas barras e , que possuem mesmo módulo e sentido contrário considerando a simetria da treliça. Para encontra-las, vamos utilizar o nó .
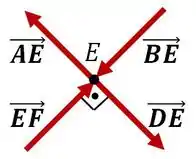
Observe que as forças são perpendiculares entre si, então simplesmente temos, pelo equilíbrio de forças:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 