Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 112

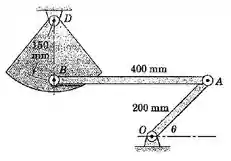
5/112) A barra O A possui uma velocidade angular no sentido anti-horário θ ' = 4   r a d / s durante um intervalo de seu movimento . Determine a velocidade angular da barra A B e do setor B D para θ = 45 ° instante em que A B está horizontal e B D está vertical .

Passo 1

Então galera , como aprendido neste capítulo , sabemos que :

v = ω r

Sendo assim , temos que :

v A = A O - θ ' = 8 4 = 32   i n / s

Como possuem um ponto em comum , sabemos que a velocidade angular de A B é igual a de A C . Logo , obtemos que :

ω A B = ω A C = v A A C - = 32 16 2 = 2 = 1,414   r a d / s     S A H

Passo 2

Bom pessoal , utilizando raciocínio análogo ao passo anterior ,temos que :

ω B C = ω A C

Ou seja ,

v B B C - = v A A C -

Logo ,

v B = B C - v A A C - = 16 16 2 32 = 22,6   i n / s

Para acharmos a velocidade angular do setor B D , por sua vez , basta aplicarmos a relação :

ω B D = v B B D - = 22,6 6 = 3,77   r a d / s   S H

Resposta

ω A B = 1,414   r a d / s     S A H

ω B D = = 3,77   r a d / s   S H

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/71) A barra C B desliza através do cursor articulado fixado à barra O A . Se C B possui uma velocidade angular no sentido horário de 2r a d / s , determine a velocidade angular ω O A da barra O A qu
5/76) No instante representado , a placa triangular A B D possui uma velocidade angular no sentido horário de 3r a d / s . Determine para esse instante a velocidade angular ω B C da barra B C .
5/105) Determine a velocidade do ponto D no Prob.5/62 pelo método da seção 5/5 .
5/104) A extremidade A da vara delgada recebe uma velocidade v A para a direita ao longo dasuperfície horizontal . Mostre que o módulo da velocidade da extremidade B é igual á v A quando o ponto centr
5/102) O eixo do conjunto da roda sem deslizar sobre a superfície horizontal fixa . e o ponto O possui uma velocidade de 0,8m / s para a direita . Pelo método dessa seção , determine as velocidades do