Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 142
Determine a expressão vetorial para o momento da força de em relação ao ponto . A especificação de projeto para o parafuso em necessitaria deste resultado.
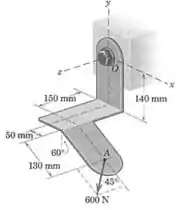
Passo 1
Vamos lembrar da definição do momento de uma força:
Onde é o vetor posição que liga a origem e o ponto onde a força é aplicada. Vamos dar uma olhada no desenho para escrever esse vetor:
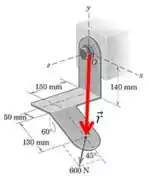
E então:
Passo 2
E vamos fazer a mesma coisa para a força :
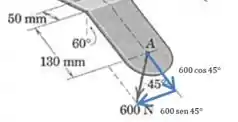
Passo 3
E agora podemos calcular o produto vetorial:
E então temos o seguinte resultado:
O momento da força é:
Resposta
O momento total da força em relação ao ponto é .
Exercícios de Livros Relacionados
57. A placa triangular A B C é sustentada por juntas rotuladas em B e D e mantida na posição mostrada pelos cabos A E e C F . Se a força exercida pelo cabo A E em A é de 55N , determine o momento dess
53. Para afrouxar uma válvula congelada, uma força F de intensidade 300N é aplicada na alavanca da válvula. Sabendo que θ = 25 ° , M x = - 83N ⋅ m , e M z = - 58N ⋅ m , determine ՓՓ e d .
52. Para o guindaste do problema 3.51 , determine a maior distância admissível x quando a tensão na linha A B A D é 267N .
54. Durante a aplicação da froça F na alavanca da válvula mostrada na figura, os seus momentos sobre os eixos x e z são, respectivamente M x = - 104N ⋅ m e M z = - 109N ⋅ m . Para d = 0,7m , determine
57. A placa triangular A B C é sustentada por juntas rotuladas em B e D e mantida na posição mostrada pelos cabos A E e C F . Se a força exercida pelo cabo C F em C é 33N , determine o momento dessa f