Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 169

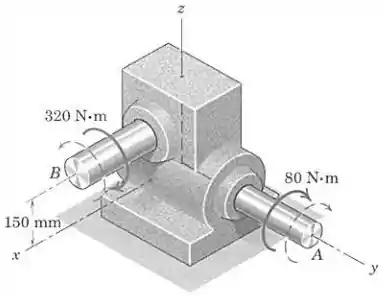
As direções de rotação dos eixos de entrada A e de saída B no redutor de engrenagens estão indicadas pelas setas curvas tracejadas. Um torque de entrada (binário) de 80   N ∙ m é aplicado ao eixo A na direção da rotação. O eixo de saída B fornece um torque de 320   N ∙ m à máquina que ele controla (que não está mostrada). O eixo da máquina exerce um torque de reação igual e contrário no eixo de saída do redutor. Determine a resultante M dos dois binários que atuam no redutor e calcule o cosseno diretor de M em relação ao eixo x .

Passo 1

Conforme mostra a figura, temos:

M x = - 320   i   N ∙ m

M y = - 80   j   N ∙ m

M z = 0

Logo,

M = - 320   i - 80   j   N ∙ m

Passo 2

Agora, vamos calcular o cosseno diretor de M em relação ao eixo x :

cos ⁡ θ x = M x M

cos ⁡ θ x = - 320 - 320 2 + - 80 2

cos ⁡ θ x = - 0,970

Resposta

M = - 320   i - 80   j   N ∙ m

cos ⁡ θ x = - 0,970

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

56. No problema 3.55 determine o momento sobre a diagonal A D exercida pela força na armação pela porção B G do cabo.
3.18. Um plano contém os vetores A e B. Determine o vetor unitário normal ao plano quando A e B são iguais, respectivamente, (a) î + 2 j ^ - 5 k ^ î e 4î - 7 j ^ - 5 k ^ î , (b) 3î - 3j ^ + 2k ^ î e -
3.17. Os vetores P e Q constituem dois lados adjacentes de um paralelogramo. Determine a área do paralelogramo quando (a) P =- 7î + 3j ^ - 3k ^ î e Q = 2î + 2j ^ + 5k ^ î , (b) P = 6î - 5j ^ - 2k ^ î
3.19. Determine o momento em relação à origem O da força F = 4î + 5j ^ + 3k ^ î que atua em um ponto A. Suponha que o vetor posição de A seja (a) r = 2î - 3j ^ + 4k ^ î , (b) r = 2î + 2,5j ^ - 1,5k ^
3.20. Determine o momento em relação à origem O da força F = - 2î + 3j ^ + 5k ^ î que atua em um ponto A. Suponha que o vetor posição de A seja (a) r =î + j ^ +k ^ î , (b) r = 2î + 3j ^ - 5k ^ î , (c)