Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 141

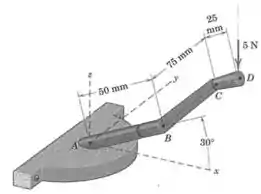
Uma força vertical de 5   N é aplicada à manete do mecanismo de abertura de janelas quando a manivela B C está na horizontal. Determine o momento da força em relação ao ponto A e em relação à linha A B .

Passo 1

Vamos lembrar da definição do momento de uma força:

M → = r → × F →

Como a força F → é paralela ao eixo z , a forma vetorial é:

F → = - 5   k ^ = - 5   k ^   N

E agora precisamos de uma expressão para o vetor r → que une os pontos A e D . É importante ver o desenho para entender essa parte, e é uma boa escrever um componente de cada vez:

r x = 50 + 25 cos ⁡ 30 ° = 64,9   m m

r y = 75   m m

r z = 50 + 25 sen ⁡ 30 ° = 37,5   m m

Então:

r → = r x   i ^ + r y   j ^ + r z   k ^

r → = 64,9   i ^ + 75,0   j ^ + 37,5   k ^   m m

Passo 2

Agora vamos calcular o produto vetorial:

M → = r → × F →

M → = 64,9   i ^ + 75,0   j ^ + 37,5   k ^ × - 5   k ^  

M → = i ^ j ^ k ^ 64,9 75,0 37,5 0 0 - 5

M → = - 5 75 i ^ - - 5 64,9 j ^

M → ≅ - 375   i ^ + 325   j ^   N   m m

Passo 3

Agora queremos encontrar o momento em relação à linha A B . Para isso precisamos primeiro escrever um vetor unitário nessa direção:

n ^ = cos ⁡ 30 ° i ^ + sen ⁡ 30 °   k ^

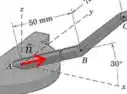
Agora é só fazer o produto escalar do nosso momento M → com esse vetor:

M A B = M → ∙ n ^

M A B = - 375   i ^ + 325   j ^ ∙ cos ⁡ 30 °   i ^ + sen ⁡ 30 °   k ^

M A B = - 375 cos ⁡ 30 ° + 325 0 + 0 sen ⁡ 30 °

M A B = - 324,7

Esse é o módulo da projeção de M → na linha A B , para encontrar a forma vetorial é só multiplicar esse módulo pelo vetor unitário n ^ :

M → A B = M A B   n ^

M → A B = - 324,7 cos ⁡ 30 ° i ^ + sen ⁡ 30 °   k ^

M → A B ≅ - 281   i ^ - 162   k ^   N   m m

Resposta

O momento em relação a A é M → A = - 375   i ^ + 325   j ^   N   m m e em relação à linha A B é M → A B = - 281   i ^ - 162   k ^   N   m m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

47. A tampa A B C D de uma caixa de engrenagem de 0,61m × 1,0m , é articulada ao longo do lado A B e mantida aberta com uma cordaD E C lançada sem atrito a um gancho em E . Sabendo-se que a tração na
51. Um pequeno barco é suportado por dois guindastes, um dos quais é mostrado na figura. Sabendo que o momento sobre o eixo z da resultante R A exercida no guindaste em A não deve exceder 378N ⋅ m em
48. A tampa A B C D de uma caixa de engrenagem de 0,61m × 1,0m , é articulada ao longo do lado A B e mantida aberta com uma cordaD E C lançada sem atrito a um gancho em E . Sabendo-se que a tração na
50. Para erguer um caixote pesado, um homem utiliza uma talha presa embaixo de uma viga I pelo gancho B . Sabendo que o homem aplica uma força de 195N a extremidade A da corda e que o momento dessa fo
55. Uma armação A C D é articulado em A e B e sustentada pelo cabo que passa através de um anel em B e fixada por ganchos em G e H . Sabendo que a tensão no cabo é de 450N , determine o momento sobre