Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 142
O poste rígido com barras cruzadas do Prob. é mostrado novamente aqui. Determine a expressão vetorial para o momento da força trativa de (a) em relação ao ponto e (b) em relação ao eixo do poste. Encontre cada momento de duas maneiras diferentes.
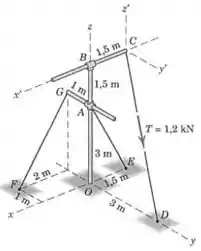
Passo 1
Para encontrar a expressão vetorial para a força , primeiro precisamos encontrar um vetor unitário na direção :
E agora para encontrar o vetor unitário é só dividir pelo próprio módulo:
E agora fica fácil encontrar a expressão para :
Passo 2
(a) Beleza, agora vamos calcular o momento de em relação ao ponto :
Onde é o vetor posição que une a origem e o ponto onde a força é aplicada (poderia ser qualquer outro ponto na linha de ação da força, mas esse é o mais conveniente):
Então o produto vetorial é:
Passo 3
(b) Agora queremos o momento dessa força em relação ao eixo do poste. A forma mais fácil de calcular isso é simplesmente projetar o vetor no eixo .
Para isso podemos usar o produto escalar:
Já que é o vetor unitário na direção do eixo :
Como o produto escalar é nulo e o produto é igual a , o momento é:
Resposta
(a) O momento em relação à origem é
(b) O momento em relação ao eixo é .