Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 43
5.43. A barra uniforme AB possui peso de . Determine a força no cabo quando a barra está na posição mostrada.
Passo 1
Cara, fala aí! A gente quer a tensão no cabo. Vamos primeiro entender o que está acontecendo.
O apoio em permite que o cabo desça, mas não permite que ele se mova na horizonta. Então a gente só tem uma reação que vamos chamar de .
Ali em , temos um apoio que só tem reação vertical. E a gente tem o peso da barra atuando em seu centroide, ou seja, na metade da barra.
E como temos o cabo na rótula, a tensão é a mesma em todo o cabo. Aí a gente pode achar o que ele pede analisando a barra . Como ela está paradinha, valem as equações de equilíbrio estático.
Um DCL do que a gente conversou
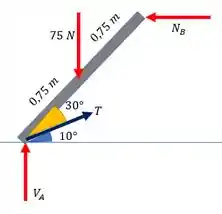
Passo 2
Beleza, como o sistema está estático, podemos dizer que
Vamos decompor as medidas da barra em relação aos eixos verticais e horizontais, para achar os braços de alavanca dos momentos. Nosso somatório do momento com relação ao ponto considerando a direção anti-horária como positivo será:
Então
Passo 3
E finalmente vamos usar a equação de equilíbrio ao longo do eixo x
Aqui a gente decompõe em relação ao eixo :
Logo