Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 48
5.44. Determine a força P necessária para puxar o cilindro de pelo degrau liso. Considere .
Passo 1
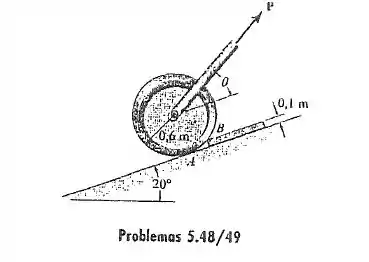
Cara, ele pediu para a gente achar que faça mover esse cilindro pelo degrau liso. O melhor é sempre começar pelo DCL para entender o que está havendo:
Esse retângulo azul é o degrau, tá? Temos o peso do cilindro para baixo que vale
Temos as forças normais de contanto em e . E temos a força orientada de .
Só que repara uma coisa, na eminência do movimento, quando o cilindro está quase saindo do lugar, a normal em zera, aí fica só como normal.
Percebe que a gente vai usar esse sistema de eixos inclinados, para facilitar as contas.
Como está tudo em equilíbrio, afinal estamos ainda na eminência do movimento, podemos usar as equações de equilíbrio de forças e momentos.
Bora lá!
Passo 2
Agora podemos usar o fato que o momento total é 0 e fazer o somatório de momentos no ponto . Aí a gente pode ignorar e achar .
Vamos decompor nossas forças em relação a e para achar os braços de alavanca certinho.
Mas antes a gente precisa achar o braço de alavanca da componente de do eixo em relação a , porque isso não tá claro na figura. Vamos reunir as informações que temos
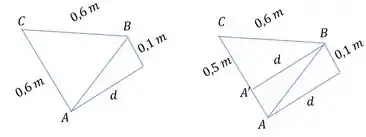
No nosso desenho é o centro do cilindro. Percebe que ali a gente tem um triângulo retângulo. Aí podemos fazer:
Isolando :
Passo 3
Agora sim, a gente a parte para o somatório de momentos
Logo