Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 78
Determine as componentes vertical e horizontal da reação nos pinos A e C da estrutura de dois membros
Passo 1
O bizu da questão é perfceber que ele pode ser simplificado se considerarmos o membro BC como um todo, com forças aplicadas em C e B.
Começamos fazendo o diagrama do corpo livre do elemento AB:
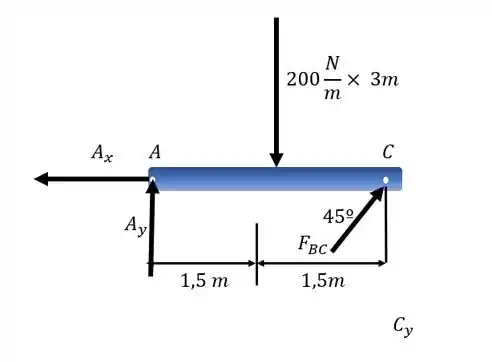
Passo 2
Podemos utilizar as equações do equilíbrio em relação ao momento para o ponto A:
Passo 3
Agora, utilizando as equações do equilíbrio no eixo y:
Passo 4
Agora, utilizando as equações do equilíbrio no eixo X:
Passo 5
Para o pino C:
Resposta
Exercícios de Livros Relacionados
O atuador pneumático em D é usado para aplicar uma força F = 200N no membro em B . Determine as componentes horizontal e vertical da reação no pino A e a força da barra lisa em C no membro.
A barra fina de comprimento l é sustentada pelo tubo liso. Determine a distância a necessária para o equilíbrio se a cara aplicada é P .
A barra uniforme, de comprimento l e peso W , está apoaida na extremidade A por uma parede lisa e na extremidade B por uma corda de comprimento s , que é presa à parede como mostra a figura. Mostre qu
Determine as componentes horizontal e vertical da reação em A e a tração no cabo B C sobre a lança ao problema 5.6 .
O vagão ferroviário possui um peso de 120k N e centro de gravidade em G . Ele é suspenso pela frente e por trás no trilho por seis pneus localizados em A ,BeC . Determine as reações normais desses pne