Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas - Ex. 28
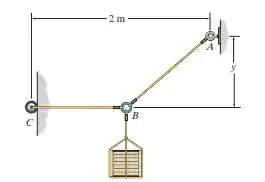
Se a corda AB de 1,5 m pode suportar uma força máxima de 3500 N, determine a força na corda BC e a distância y, de modo que a caixa de 200 kg possa ser suportada.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como está com essa pandemia?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual a força a partir do eixo. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser lembrar que, pela equação de equilíbrio, a soma das forças no eixo tem que ser igual a zero.
Já temos meio passo andado. Vamos calcular para o outro eixo.
Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e achar nossos valores!!