5.4748. Determine the coordinates of the centroid of the shaded area.
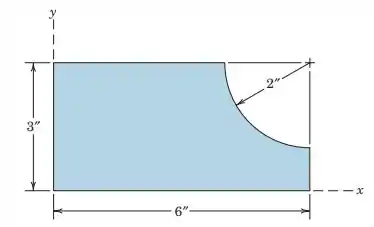
Passo 1
Para encontrar as coordenadas do centroide podemos usar as equações
Mas esse problema aqui vai simplificar as coisas para a gente, porque a densidade é homogênea. Então ficamos com
Passo 2
Beleza, vamos fragmentar o problema em três figuras mais fáceis de resolver
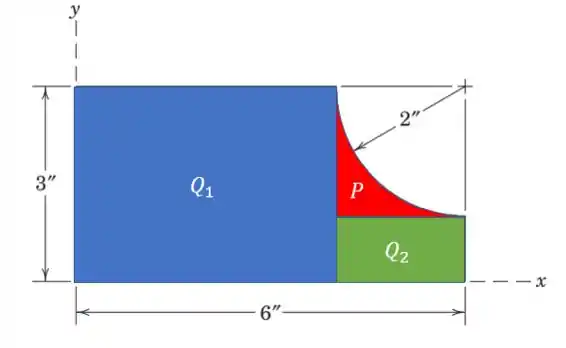
Vamos começar com o retângulo .
E
Agora temos as coordenadas do centroide do retângulo.
E a área fica o seguinte
Passo 3
Agora vamos para o retângulo , e para facilitar os cálculos vamos fazer uma mudança de coordenadas, agora a origem é na ponta do retângulo
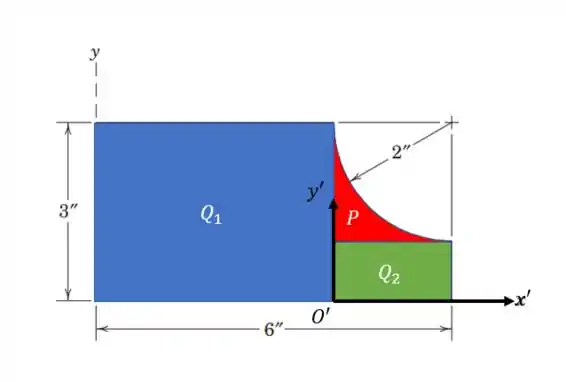
A equação dessas coordenas fica
Vamos lá.
E a área dessa figura é
Agora vamos colocar nas coordenadas originais
Passo 4
Agora podemos finalmente usar a equação
E essa equação vira
Vamos substituir os valores na equação
E agora vamos fazer para o eixo
Substituindo os valores
Então o ponto do centroide é
agora vamos para a figura mais complicada, a parábola. Mas a gente pode simplificar, olha só, a parábola pode ser uma subtração de imagens, imagina que a gente tem um retângulo, e subtrai um quarto de um circulo desse quadrado, ficamos com uma parábola.


Vamos trabalhar então. O nosso novo sistema de coordenadas é:
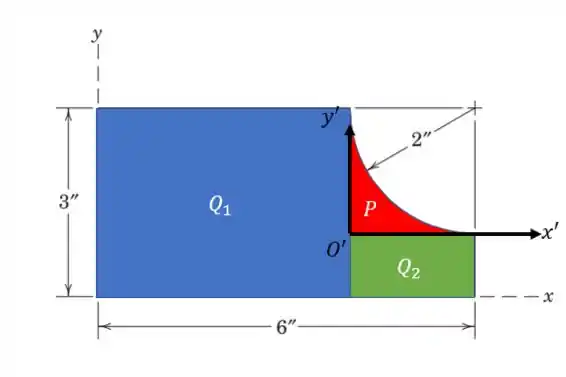
Mas vamos começar calculando a área. A área da parábola é a área do quadrado menos a área da fração de círculo. A área do quadrado é
E a área da fração de círculo é
Então
Agora vamos calcular os centroides, para o quadrado é
E para a fração de círculo
Então o centroide da parábola fica
Então
Então
E olha só, isso vai ser o mesmo para , porque tanto o quadrado quando a fração de círculo são simétricos.
Agora vamos passar isso para as coordenadas originais.
E
Passo 5
Só falta a gente calcular o centroide da figura toda agora
Substituindo os valores
Fazendo essa conta chegamos em
Agora vamos fazer para
Substituindo os valores
E ficamos com