Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 40

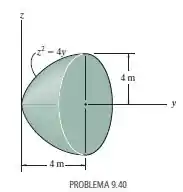
Localize o centroide overset(-)(y) do paraboloide.

Passo 1

Oi tudo bem? Vamos resolver este exercício.

Vamos analisar a figura a seguir:

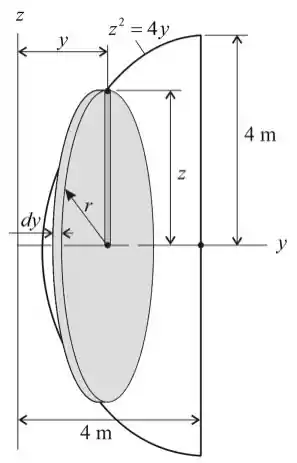
Passo 2

Vamos considerar uma forma elementar de disco fino de espessura d y e localizado a uma distância de y do eixo z .

Dada equação z^2 = 4 y

O volume desse elemento é d V = (pi z^2) d y

Sabemos que:

bar y = (int_0^4 y d V)/(int_0^4 d V)

bar y = (int_0^4 y ( pi z^2 ) d y)/(int_0^4 (pi z^2) d y)

bar y = (int_0^4 y (4 pi y) d y)/(int_0^4 (4 pi y) d y)

bar y = (4 pi int_0^4 y^2 d y)/(int_0^4 y d y)

bar y = ([(y^3)/(3)]_0^4)/([(y^2)/(2)]_0^4)

bar y = ((1)/(3) [4^3 - 0])/((1)/(2) [4^2 - 0])

bar y = (2 (64))/(3 (16))

bar y = 2.67 m

Resposta

bar y = 2.67 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23- Use os resultados do Exemplo 5/3 para calcular as coordenadas do centro de massa da parte mostrada do cilindro sólido homogêneo.
22- Determine a coordenada y do centroide da área sombreada.
24- Determine as coordenadas do centroide da área sombreada
25- Determine as coordenadas x e y do centroide da área sombreada.
2- Faça com seu lápis um ponto sobre a posição da sua melhor estimativa visual do centroide da área do setor circular. Verifique sua estimativa usando os resultados do Exercício 5/3.