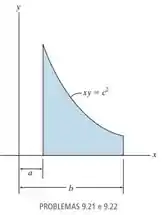
Localize o centroide da área.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Nesse problema temos uma figura hachurada que é descrita pela equação
Definida entre e .
A partir daí temos que encontrar seu centroide .
Tem ideia de como fazemos isso?
Para encontrar a coordenada do centroide de uma figura podemos aplicar a seguinte fórmula:
Em que é a área da figura.
Bora começar!
Passo 2
Vamos começar calculando a área da figura.
Pra isso podemos isolar em um lado da igualdade como:
Assim, se é definido entre e , temos que:
Calculando a integral, vamos chegar em:
Tranquilo até aqui?
Passo 3
Agora temos que calcular a integral
Como , temos:
Como é definido entre e ...
E finalmente, substituindo na fórmula de :
E fim! Entendeu tudo? Responde Aí!