Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 36

Localize o centroide overset(-)(y) da área sombreada.

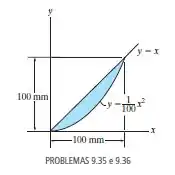
Passo 1

Oi tudo bem? Vamos resolver este exercício, começando pela parte de escrever a equação da área colorida ali.

y_2 = x

y_1 = (1)/(100) x^2

d A = (y_2 - y_1) d x

d A = (x - (x^2)/(100)) d x

overset(-)(y) = y_1 + ((y_2 - y_1)/(2)) = (y_2 + y_1)/(2)

overset(-)(y) = (x)/(2) + (x^2)/(200)

Substituindo os dados, temos que:

overset(-)(y) = (int overset(-)(y) d A)/(int d A)

int overset(-)(y) d A = int ((x)/(2) + (x^2)/(200)) (x - (x^2)/(100)) d x

int overset(-)(y) d A = (200000)/(3)

int d A = int (x - (x^2)/(100)) d x

int d A = (5000)/(3)

Passo 2

Agora vamos só jogar nossos valores na formulinha:

overset(-)(y) = (int overset(-)(y) d A)/(int d A)

overset(-)(y) = (200000)/(3) xx (3)/(5000)

overset(-)(y) = 40 m m

Resposta

overset(-)(y) = 40 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11- Determine as coordenadas x e y do centroide da área trapezoidal.
15- A massa por unidade de comprimento da barra esbelta varia com a posição de acordo com ρ = ρ 1 - x 2 , onde x está em metros. Determine a localização do centro de massa da barra.
13- Localize o centroide da área sombreada
14- Localize o centroide da área sombreada mostrada.
17- Determine as coordenadas do centroide do segmento da área.