5.50. Determine the y-coordinate of the centroid of the shaded area. 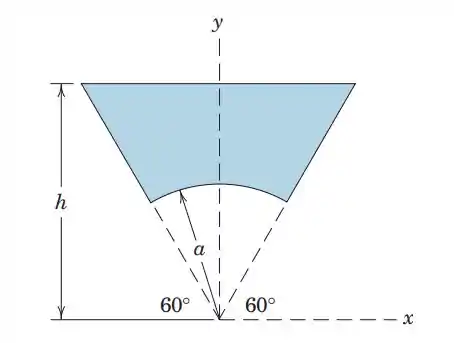
Passo 1
Vamos achar outro centroide, mas agora é só para o eixo .
Beleza, vamos fragmentar o problema em duas figuras mais fáceis de resolver

Olha só, temos duas figuras aqui, um triângulo, que é a parte azul da figura, e em cima desse triângulo temos a parte de um círculo. Bom, a gente sabe que uma linha reta tem , então a parte do círculo tem , e como um círculo completo tem , essa parte do círculo tem da área de um círculo completo.
Mas atenção, a fração de círculo não está na figura original, então tudo que fizermos em relação a ele será negativo.
Passo 2
Vamos começar com o triângulo. A área do triângulo é
A gente conhece o valor de , agora o valor de a gente ainda não sabe, mas não vai ser complicado calcular esse valor. Olha só, se cortamos o triângulo exatamente no eixo vamos ter um triângulo retângulo de cada lado, e esses triângulos vão ter os catetos e .
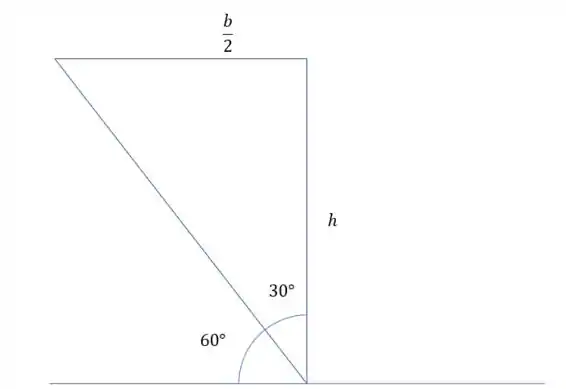
Então podemos ver que
Logo
Então a área do triângulo é
Agora vamos calcular o centroide de nesse triangulo.
Passo 3
É hora de focar na parte de círculo. Bom, a área é de um círculo completo como já vimos, então
Onde é o raio do círculo.
La no problema de exemplo 5/2, podemos ver que o centroide de uma fração de um círculo é
Nesse caso , ou seja .
Então
Então
Passo 4
Agora vamos calcular o centroide da figura toda.
Isso fica
Então
Vamos multiplicar em a fração por
Agora vamos multiplicar por
Agora podemos dividir em cima e em baixo a fração por 3
E finalmente chegamos na resposta.