Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 43
O freio de bloco de alavanca única impede a rotação do volante sob um torque no sentido anti-horário M. Encontre a força P necessária para evitar a rotação se o coeficiente de atrito estático for μs. Explique o que aconteceria se a geometria permitisse que b fosse igual a μ8.
Passo 1
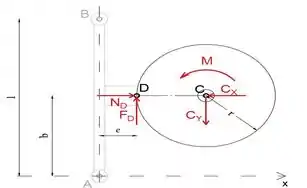
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da roda
Uma vez que a força FD é a força de atrito máxima, podemos escrevê-la como
Podemos expressar ND
(1)
Passo 2
Ao igualar a soma dos momentos sobre o ponto C a zero, podemos escrever a força FD como função do par M
Podemos substituir FD na expressão (1) pela expressão (2)
(3)
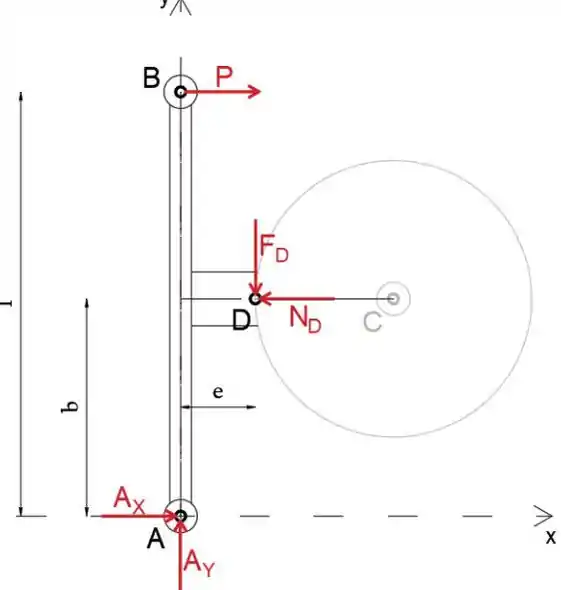
Agora, vamos isolar e desenhar o diagrama de corpo livre do membro AB
Passo 3
Equacionando a soma dos momentos sobre o ponto A a zero, determinaremos a força P
Substituiremos FD e ND nas expressões (2) e (3) respectivamente
Substituiremos .e na expressão final
Isso significa que a roda não girará, uma vez que não há força necessária para parar a rotação