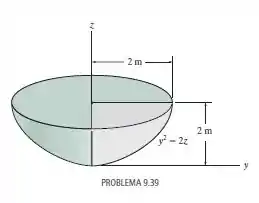
Localize o centro de gravidade do volume. O material é homogêneo.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Nesse problema foi dado um objeto e nosso objetivo é calcular seu centro de gravidade.
Lembra como fazemos isso?
Para calcular o centro de gravidade de um objeto podemos fazer:
Saca só!
Passo 2
Perceba que o objeto é simétrico ao redor do eixo , com isso, como o objeto é homogêneo podemos dizer que:
Assim nosso problema se reduz a:
O elemento infinitesimal pode ser calculado como:
Já que a casca inferior tem uma simetria circular no plano .
Porém, na figura do problema diz que
Ou seja:
Tranquilo até aqui?
Passo 3
Agora que temos nosso elemento infinitesimal podemos calcular as integrais:
Com isso, o centro geometrico no eixo é:
E aí! entendeu tudo? Responde Aí!