Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 51
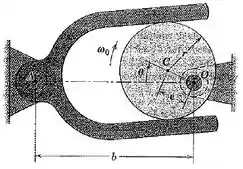
5/51) O mecanismo é projetado para produzir pequenas oscilações do eixo e do garfo anexo através da rotação do came circular deslocado , que gira em torno de com uma velocidade angular constante . Determine uma expressão para a velocidade angular do garfo e seu eixo como uma função do ângulo do came .
Passo 1
Então galera , seja o ângulo formado entre a linha e o eixo horizontal . Analisando a figura fornecida pelo enunciado , achamos que a velocidade angular da linha é a mesma do garfo , cujos lados são paralelos a . Logo ,
Sendo assim ,
Substituindo , obtemos que :
Onde ,
Resposta
Suave galera? Então bora pra próxima!!!
Exercícios de Livros Relacionados
A roda está rolando sem deslizar com uma velocidade angular ω . Admitindo que a linha P O C gire através de um ângulo diferencial d θ durante um intervalo de tempo d t , mostre que a velocidade do pon
O cursor A se desloca com velocidade constante v sobre a reta guia por um curto intervalo, enquanto o cursor B se desloca sobre a guia circular cujo centro está em O . Determine a velocidade angular ω
O ponto A recebe uma aceleração constante a para a direita a partir do repouso com x essencialmente nulo. Determine a velocidade angular ω da barra A B em termos de x e a .
28. . Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 50 ω 0,5r a d / s 2 , onde w é dado em rad/s. Determine a velocidade angular e o deslo
27. Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 450 t 2 + 60r a d / s 2 , onde t é dado em segundos. Determine a velocidade angular e o