Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 30
O cursor se desloca com velocidade constante sobre a reta guia por um curto intervalo, enquanto o cursor se desloca sobre a guia circular cujo centro está em . Determine a velocidade angular da haste de conexão em função do deslocamento do cursor .
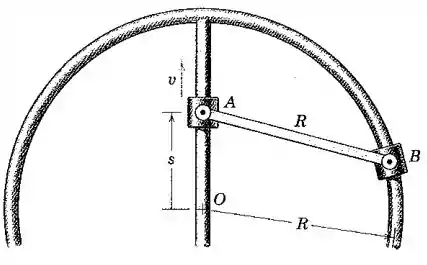
Passo 1
Na figura a seguir, podemos visualizar o ângulo que a haste de conexão faz com a horizontal, já estabelecendo uma simetria:
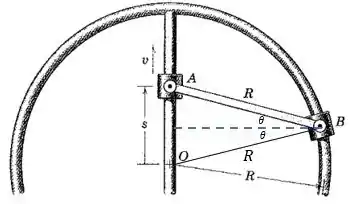
Então, pela figura, temos:
Derivamos a equação obtida em relação ao tempo:
Passo 2
Mas e , então:
Ainda temos:
Logo,
Resposta
Exercícios de Livros Relacionados
55. O pinhão A roda sobre a cremalheiras B e C. Se B está se deslocando para a direita a 2,4 m/s e C está deslocando para a esquerda a 1,2 m/s, determine a velocidade angular do pinhão e a velocidade
58. Uma bola de boliche é lançada na pista com um efeito de rotação para trás ( backspin ) ω = 10r a d / s enquanto seu centro O tem uma velocidade para frente v o = 8m / s . Determine a velocidade do
57. Resolva o problema anterior supondo que o cabo está enrolado em torno da engrenagem no sentido oposto, de maneira que a extremidade do cabo permanece horizontalmente tangente ao núcleo interior em
56. A engrenagem repousa em uma cremalheira horizontal fina. Um cabo está enrolado em torno do núcleo interno da engrenagem de maneira que ele permanece horizontalmente tangente ao núcleo interior em
Os componentes da transmissão do motor elétrico de uma locomotiva diesel elétrica são apresentados. A engrenagem tubular é solidária à roda de 1000m m de diâmetro e é acionada pelos pinhões dos dois m