Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 29

O ponto A recebe uma aceleração constante a para a direita a partir do repouso com x essencialmente nulo. Determine a velocidade angular ω da barra A B em termos de x e a .

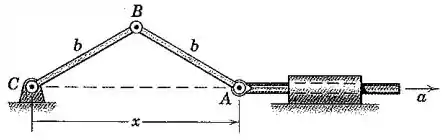
Passo 1

Observe que o ângulo θ que a barra A B faz com a horizontal é igual ao ângulo que a barra B C faz com a horizontal, pois temos uma configuração de triângulo isósceles:

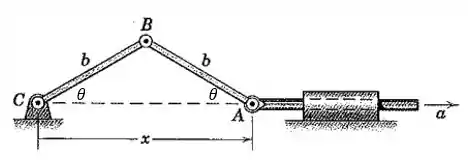
Então, pela figura, temos:

x 2 = b cos ⁡ θ

x = 2 b cos ⁡ θ

Passo 2

Derivamos a equação obtida em relação ao tempo:

x ˙ = 2 b   - s e n   θ   θ ˙

Mas ω = θ ˙ , então:

ω = - x ˙ 2 b   s e n   θ

Porém, como temos aceleração constante x ¨ = a , podemos usar uma equação do movimento uniformemente acelerado:

v 2 - v 0 2 = 2 a d

x ˙ 2 - 0 2 = 2 a x

x ˙ = 2 a x

Então:

ω = - 2 a x 2 b   s e n   θ

Passo 3

Ainda precisamos eliminar s e n   θ da nossa expressão de ω , pois θ não foi dado pelo enunciado. Mas lembre-se que obtivemos no P a s s o   1 :

x = 2 b cos ⁡ θ

cos ⁡ θ = x 2 b

Então:

s e n   θ = 1 - cos 2 ⁡ θ

s e n   θ = 1 - x 2 b 2

Logo,

ω = - 2 a x 2 b   s e n   θ = - 2 a x 2 b 1 - x 2 b 2

ω = - 2 a x 4 b 2 - x 2

O sinal negativo se deve ao fato de que o ângulo θ está diminuindo (em módulo). Se quisermos adotar o sentido anti-horário como positivo, isso se inverteria:

ω = 2 a x 4 b 2 - x 2

Resposta

ω = 2 a x 4 b 2 - x 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carretel de cabo telefônico rola sem deslizar sobre a superfície horizontal. Se o ponto A no cabo possui uma velocidade v A = 0,8m / s para a direita, calcule a velocidade do centro O e a velocidade
A lança O A está sendo elevada pelo arranjo de cabo e polia mostrado. Se o ponto B no cabo recebe uma velocidade constante v B = 3,2m / s , determine a velocidade angular ω e a aceleração angular ∝ da
O movimento do volante enquanto rola para cima a cremalheira fixa sobre o seu núcleo dentado é controlado por meio do cabo periférico pela roda motora D , que gira no sentido anti-horário na taxa cons
O movimento vertical da plataforma de trabalho é controlado pelo movimento horizontal do pino A . Se A possui uma velocidade v 0 para a esquerda, determine a velocidade vertical v da plataforma para q
Calcule a velocidade angular ω da barra esbelta A B como uma função da distância x e da velocidade angular constante ω 0 do tambor.