Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 28
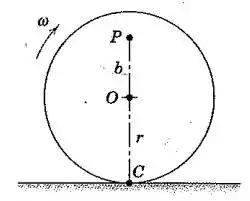
A roda está rolando sem deslizar com uma velocidade angular . Admitindo que a linha gire através de um ângulo diferencial durante um intervalo de tempo , mostre que a velocidade do ponto é igual a sua distância a partir do ponto de contato multiplicada pela velocidade angular da roda. Expresse também a velocidade de em termos da velocidade do centro .
Passo 1
Quando a linha gira através de um ângulo diferencial , o ponto se move uma distância diferencial , e o ponto , , conforme mostra a figura a seguir:
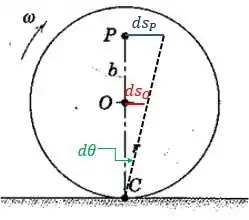
Então, pela figura, temos:
Passo 2
Podemos também expressar a velocidade em função de . Pela figura, temos:
Resposta
Exercícios de Livros Relacionados
37. O andaime S é erguido deslocando o rolete A na direção do pino em B. Se A está se aproximando de B com uma velocidade de 1,5 m/s, determine a velocidade na qual a plataforma levanta como uma funçã
45. No instante que θ = 30 ° , a manivela AB gira com uma velocidade angular e aceleração angular de ω = 10 r a d s e α = 2 r a d s 2 ,r e s p e c t i v a m e n t e . Determine a velocidade e aceleraç
50. O pino B fixado à manivela AB desliza nas ranhuras montadas nas barras seguidoras, que se deslocam ao longo das guias vertical e horizontal. Se a manivela gira com uma velocidade angular constante
36. A barra CD pressiona contra AB, fornecendo a ela uma velocidade angular. Se a velocidade de AB é mantida em ω = 5 r a d s , determine a intensidade necessária da velocidade v de CD como uma função
49. O pino B fixado à manivela AB desliza nas fendas montadas nas barras seguidoras, que se deslocam ao longo das guias vertical e horizontal. Se a manivela gira com uma velocidade angular constante ω