Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 56

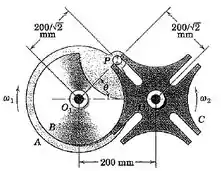
5/56) A roda de Genebra é um mecanismo para produzir rotação intermitente . O pino P naunidade integrada pela roda A e placa de travamento B encaixa na ranhura radial na roda C girando , desse modo , a roda C de um quarto de uma volta para cada rotação do pino . Na posição de encaixe mostrada , θ = 45 ° . Para uma velocidade angular constante no sentido horário ω 1 = 2   r a d / s da roda A , determine a velocidade angular correspondente no sentido anti-horário ω 2 da roda C para θ = 20 ° . (Observe que o movimento durante o encaixe é regido pela geometria do triângulo O 1 O 2 P com θ variando .)

Passo 1

Então galera , aplicando a lei dos senos ao triângulo indicado no enunciado , temos que :

b 2 sen ⁡ β = b sen ⁡ π - θ - β = b sen ⁡ θ + β

Então ,

2 sen ⁡ β = sen ⁡ θ + β

Logo ,

2 β ' cos ⁡ β = θ ' + β ' cos ⁡ θ + β

Passo 2

Bom pessoal , pelas equações que aprendemos nesta relação , temos que a velocidade angular da placa de travamento é dada por :

ω 2 = - β = θ ' cos ⁡ θ + β cos ⁡ θ + β - 2 cos ⁡ β

Sendo assim , através da relação sen ⁡ β 2 - cos ⁡ θ = sen ⁡ θ cos ⁡ β , obtemos que :

tan ⁡ β = sen ⁡ θ 2 - cos ⁡ θ

Logo , para θ = 20 °

β = tan - 1 ⁡ 0,3420 2 - 0,9397 = tan - 1 ⁡ 0,7208 = 35,8 °

Passo 3

Bom galera , além disso para θ ' = - 2   r a d / s , a equação da velocidade angular para a placa de travamento indicada no passo anterior nos dá que :

ω 2 = - 2 cos ⁡ 20 ° + 35,8 ° cos ⁡ 20 ° + 35,8 ° - 2 cos ⁡ 35,8 °

Sendo assim , temos que :

ω 2 = - 2   0,5623 - 0,5849 = 1,923   r a d / s

Resposta

ω 2 = 1,923   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/54) Mostre que as expressões v = r ω e a t = r α , são válidas para o movimento do centro O da roda querola sobre o arco circular côncavo ou convexo , onde ω e α são a velocidade e a aceleração angu
5/47) O braço ranhurado gira em torno de O e mantém a direção entre os movimentos dos cursores A e B e de suas barrasde controle . Cada pequeno bloco articulado está preso ao seu respectivo cursor e é
Determine a aceleração do eixo B para o θ = 60 ° se a manivela O A possui uma aceleração angular θ ¨ = 8r a d / s 2 e uma velocidade angular θ ˙ = 4r a d / s nessa posição. A mola mantém o contato ent
5/57) O punção é acionado por uma oscilação harmônica simples do setor articulado dada por θ = θ 0 sen ⁡ 2 π t , onde a amplitude é θ 0 = π 12r a d( 15 ° ) e o tempo para uma oscilação completa é de 1