Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 59
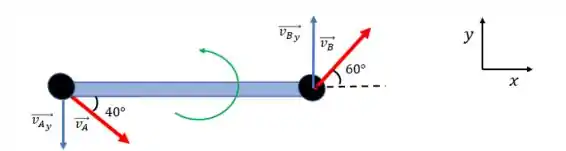
5/59) A extremidade da haste possui a velocidade indicada no instante representado . A extremidade está confinada a se deslocar na ranhura. Para esse instante calcule a velocidade de e a velocidade angular de .
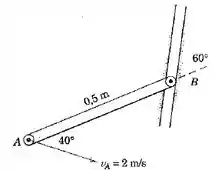
Passo 1
Bom galera , pela relação indicada nesta seção do livro , temos que :
Agora vamos fazer um esquema que mostre melhor a geometria do problema:
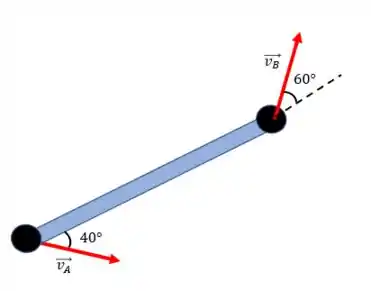
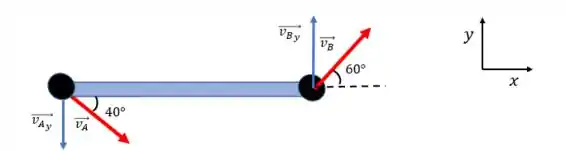
Agora vamos girar essa figura para facilitar a visualização do que eu vou falar e adotar eixos coordenados:
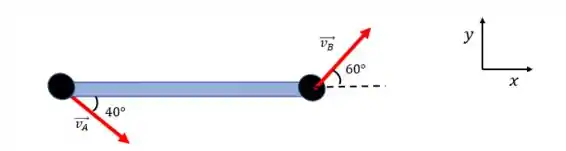
Agora, pensa comigo: se eu decompor na diração essas componentes precisam ser iguais, certo?
Sabe qual o motivo? Porque a barra não pode se esticar nem se comprimir, já que é um objeto rígido. Assim, na direção axial, não pode existir uma diferença de velocidade, e isso só pode ser garantido se as componentes das velocidades em e em nessa direção forem as mesmas.
Em outras palavras:
Como
Portanto:
Passo 2
Beleza, mas e a velocidade Como vimos, na direção não pode haver diferença nas velocidades. Porém, na direção sim, pois, afinal de contas, isso acaba gerando um movimento rotacional na barra:
Assim, podemos escrever que:
Pela relação com os ângulos do desenho:
Só que aponta na direção contrária ao eixo , né? Então:
Assim:
Logo , temos que :
Além disso , nós sabemos que :
Afinal de contas, como foi falado, essas velocidade vai gerar uma rotação na barra.
Sendo assim:
Anti-horário? Sim, basta observar a figura novamente:
