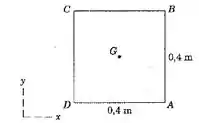
5/68) A placa quadrada uniforme se desloca no plano e possui uma velocidade angular no sentido horário . No instante representado , o ponto tem uma velocidade de para a direita , e a velocidade de , em relação a um observador sem rotação em , tem o módulo de . Determine as expressões vetoriais para a velocidade angular da placa e a velocidade do seu centro .
Passo 1
Bom pessoal , como visto anteriormente , sabemos que :
Logo ,
Passo 2
Então galera , agora para acharmos a velocidade do centro , basta aplicarmos a relação :
Logo ,
Sendo assim ,