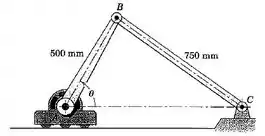
5/73) A unidade em consiste em um motor com redução de alto torque que gira a barra na taxa constante . A unidade é livre para se mover ao longo da superfície horizontal . Determine a velocidade da unidade quando atinge .
Passo 1
Fala meu povo, tudo certo? Nossa meta aqui é encontrar a velocidade em A e para isso vamos precisar definir os ângulos do problema e fazer algumas relações trigonométricas.
Lembrando que:
Vamos fazer um desenho e nomear nossos ângulos, vai facilitar bastante a nossa vida.
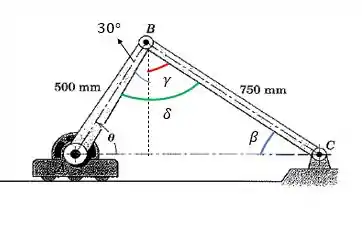
Passo 2
Como a gente falou, vamos definir esses ângulos aqui começando pelo
Aplicando a lei dos senos ao triângulo indicado na figura , obtemos que :
Isolando o seno de beta, temos;
E fazendo a inversa temos:
Logo ,
Pela trigonometria da figura em questão , obtemos que :
E por fim o delta.
Esses ângulos vão nos ajudar a encontrar uma relação entre as velocidades.
Passo 3
Partindo pras velocidades a velocidade de em relação a é dada por :
Onde
Aplicando a lei dos senos mais uma vez, obtemos que ;
Logo: