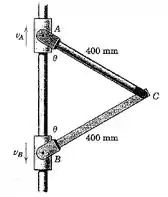
5/63) Por um curto intervalo , os cursores e estão deslizando ao longo do eixo fixo vertical com velocidade e nos sentidos indicados . Determine o módulo da velocidade do ponto para a posição .
Passo 1
Então galera a gente tem que lembrar de uma propriedade de velocidade relativa:
Ou seja, a velocidade de um ponto é a velocidade de um ponto mais a velocidade relativa entre eles. Isso funciona para quaisquer pares de pontos.
Passo 2
Vamos fazer um desenho das velocidades para entender um pouco melhor:
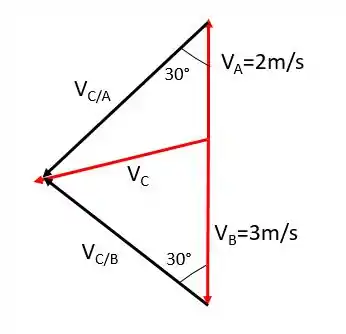
Passo 3
Agora analisando a geometria da figura, vamos ter:
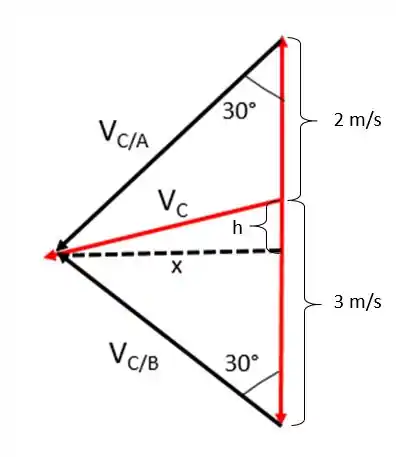
Reparem que é um triângulo isósceles, logo a altura é, também, mediana, portanto divide o lado da direita ao meio. Como esse lado equivale a unidades então a marcação pontilhada divide em dois lados de . Como mostrado abaixo:
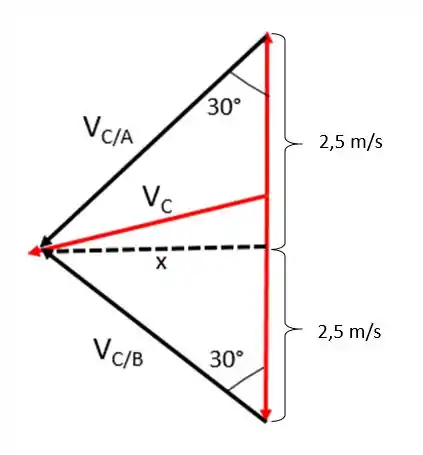
Agora a gente só precisa achar , que pode ser obtido pela tangente de 30°, olhando o triângulo de lados ():
para finalizar a gente faz Pitágoras no triângulo (). Reparando que
obs: porque quando fizemos a divisão do triângulo ficou:
Voltando ao cálculo por Pitágoras: