Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 93
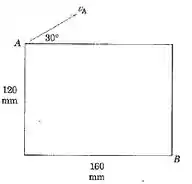
5/93) Para o instante representado , o vértice da placa retangular possui uma velocidade e a placa possui uma velocidade angular no sentido horário . Determine o módulo da velocidade correspondente do ponto .
Passo 1
Então galera , a primeira coisa que devemos achar é a distância do ponto até o centro instantâneo de velocidade nula do sistema . E para isso , sabemos que :
Logo ,
Passo 2
Bom pessoal , agora bora dar uma olhada na situação do problema:
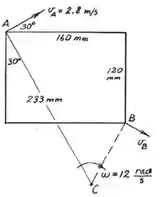
Sendo assim , para acharmos a distância entre o ponto e o centro instantâneo da velocidade basta aplicarmos a relação :
Logo ,
Agora tudo fica mais fácil . Como já sabemos a velocidade angular do sistema , podemos achar o módulo da velocidade do ponto através da equação :
Resposta
Exercícios de Livros Relacionados
A placa mostrada na figura desloca-se no plano x y . Sabendo que v A x = 300m m / s, v B x = - 100m m / s e v C y = - 600m m / s , determine ( a ) a velocidade angular da placa, ( b ) a velocidade do
A barra A B movimenta-se sobre um rolete em C enquanto a extremidade A desloca-se para a direita com velocidade constante de 500m m / s . No instante mostrado na figura, determine ( a ) a velocidade a
15.47. No Problema 15.46, determine (a) a velocidade do ponto B, (b) o ponto da placa com velocidade nula.
15.49. No sistema de engrenagens planetárias mostrado na figura, o raio da engrenagem central A é a, o raio das engrenagens planetárias é b e o raio da engrenagem externa E é a +-2b. A velocidade angu
15.46. A placa mostrada na figura desloca-se no plano xy. Sabendo que (vA)x 120 mm/s, (vB)y 300 mm/s e (vC)y 60 mm/s, determine (a) a velocidade angular da placa, (b) a velocidade do ponto A.