Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 59
59- Um tetaedro regular tem seis arestas de comprimento . Uma força é dirigida ao longo da aresta , como mostrada na figura. Determine o momento de em relação a aresta .
Passo 1
A essa altura do livro espero que você já tenha entendido um pouco sobre como se calcula o momento em relação a um eixo (ou a uma linha), sabemos que precisaremos de três vetores. O vetor diretor do eixo que queremos calcular o momento, um momento de distância relativa de um ponto do vetor onde encontra-se a força para um ponto do eixo onde queremos calcular o momento e o vetor da força. Bem, com isso vamos escolher os vetores que usaremos:
Vetor onde queremos saber o momento
Vetor de distância relativa:
Vetor onde se encontra a força
Sabendo que todos os lados do tetraedro são iguais, isso nos diz que todos os triângulos formados na figura são equiláteros podendo ser desenhados da seguinte forma:
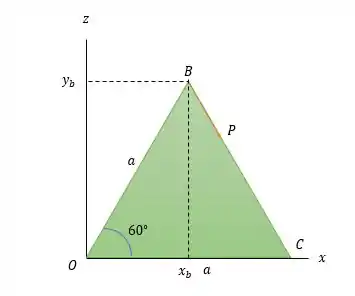
Assumindo que o eixo tem coordenadas nos três eixos (por que no desenho não fica claro né)
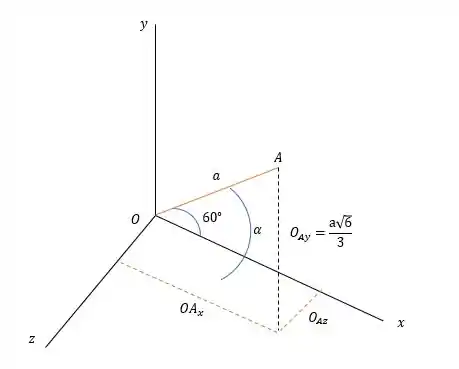
Pois a altura de um tetraedro regular é
Passo 2
Das figuras do passo conseguimos tirar os vetores que precisamos:
Agora para o vetor força:
Lembrando que F se normaliza também.
E o vetor será calculado da seguinte forma:
Passo 3
Montando a matriz nós teremos:
Resolvendo essa determinante nós temos: