Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 61
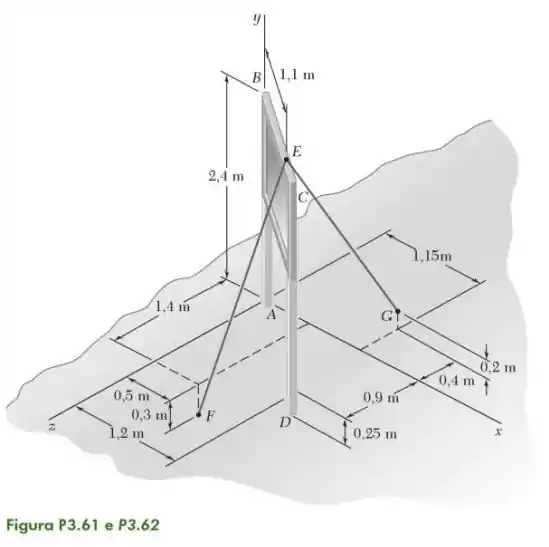
61- Uma placa de sinalização é erguida em um terreno desnivelado e ancorada pelos cabos e . Se a força exercida pelo cabo em é , determine o momento desta força sobre a linha que une os pontos e .
Passo 1
Vamos vetorizar a força que passa sobre indo de até . Mas primeiro vamos calcular a angulação que faz no plano em relação ao eixo . O ponto está no ponto cartesiano igual a:
Em relação a o ângulo que a reta faz é de:
Passo 2
Então com isso conseguimos vetorizar as forças e as distâncias
A força vetorizada será:
Nós vamos considerar o sinal negativo para a força pois vamos fazer ela saindo da base para calcular o momento, e essa força suportada pelo chão será negativa para que a corda fique estática.
Isso será:
Passo 3
Agora precisaremos vetorizar o eixo e isso nos dará:
E a distância relativa da força ao eixo que vamos fazer aqui é a distância entre o ponto e o ponto . E que será a distância relativa de até :
Passo 4
O que faz com que a determinante do momento seja:
Fazendo essa determinante nós encontramos: