Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 24
24- Uma tábua , usada para escorar temporariamente um telhado, exerce no ponto do telhado uma força de dirigida ao longo de . Determine o momento de força em relação a .
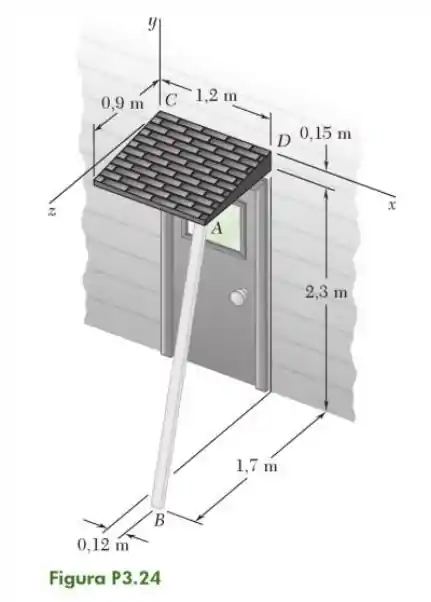
Passo 1
Teremos o seguinte diagrama de forças na tábua.
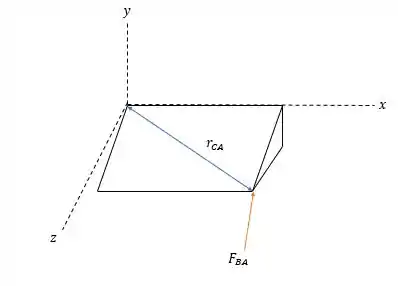
Aí para descobrir vetor do momento em relação a teremos que saber o vetor direção da força em relação a e o vetor da força e elas serão dadas da seguinte forma:
Pois é a variação de para respeitando o sentido dos vetores ordenados. Isso nos dá:
Agora o vetor que nos diz a distância de para é:
Passo 2
Dessa forma montando a matriz para encontrar o momento temos:
Resolvendo esse determinante temos:
Resposta
Exercícios de Livros Relacionados
Calcule a força na conexão A B das garras de elevação que se cruzam sem se tocar.
Os elementos de um mecanismo acionados por uma mola, da tampa do porta-malas de um carro, estão mostrados na figura. Para a posição de equilíbrio mostrada, determine o momento M A que cada uma das mol
Determine a força de aperto vertical em E em termos da força P aplicada ao cabo do rebitador.
A morsa com dois atuadores mostrada na figura é usada para dar uma força de aperto adicional quando os parafusos são apertados. Se o parafuso vertical é apertado para produzir uma força de aperto de 3
A máquina mostrada é usada para mover itens pesados, tal como estrados de tijolos, em locais de construção. Para a posição horizontal mostrada da lança, determine a força em cada um dos dois cilindros