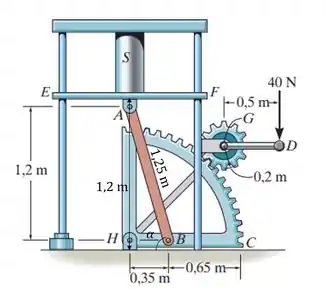
6.112. O cabo da prensa de setor é fixado na engrenagem G, que, por sua vez, está engrenada com o setor de engrenagem C. Observe que a barra AB possui pinos em suas extremidades conectando-a com a engrenagem C e com a face inferior da plataforma EF, que está livre para se mover verticalmente devido às guias lisas em E e F. Se as engrenagens exercem apenas forças tangenciais entre elas, determine a força de compressão desenvolvida sobre o cilindro S quando uma força vertical de é aplicada no cabo da prensa.
Passo 1
Precisamos determinar a força de compressão para isso vamos precisar determinar algumas forças que agem no sistema, uma que podemos determinar inicialmente é para isso precisamos analisar o ponto G. Então
Então
Passo 2
Agora podemos determinar , para isso vamos analisar o ponto A
Passo 3
Finalmente temos o necessário para determinar
Então