Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 55
A porta de carga para um avião de seção circular da fuselagem consiste na carenagem semicircular uniforme de massa . Determine a compressão na escora horizontal em para manter a porta aberta na posição mostrada. Encontre também uma expressão para a força total suportada pela dobradiça em . (Consulte a Tabela D/3 do Apêndice D para a posição do centróide ou centro de massa da capota.)
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a compressão no ponto necessária para manter a porta aberta na posição mostrada e uma expressão para a força suportada pela dobradiça em . Para começar a resolver nosso problema, vamos primeiro fazer o diagrama de corpo livre.
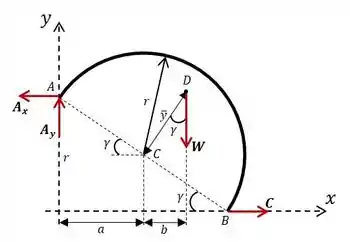
Precisamos então definir algumas variáveis, a começar pela posição do centro de gravidade em :
O ângulo de inclinação do semicírculo:
A distância horizontal entre o eixo e o centro do semicírculo em :
E, finalmente, a distância horizontal entre o centro do semicírculo em o centro de gravidade em :
Passo 2
Show, feito isso, temos tudo que precisamos para determinar a compressão , basta calcularmos o somatório de momentos em torno do ponto que deve ser nulo para que o corpo esteja em equilíbrio.
Passo 3
Agora só temos as reações e para descobrir. Para isso, uma vez que temos todas as demais forças, podemos usar as equações de equilíbrio de forças nas direções e . Começando pela direção :
E na direção :
Com isso, o módulo da força total suportada em é dada por:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 